Radioaktivní rozpad (10/10) · 10:16
Radioaktivní rozpad a semilogaritmické grafy Ukážeme si, jak odvodit vztah mezi rozpadovou konstantou k a poločasem rozpadu. Použijeme semilogaritmický graf, který nám dá lineární závislost se směrnicí -k.
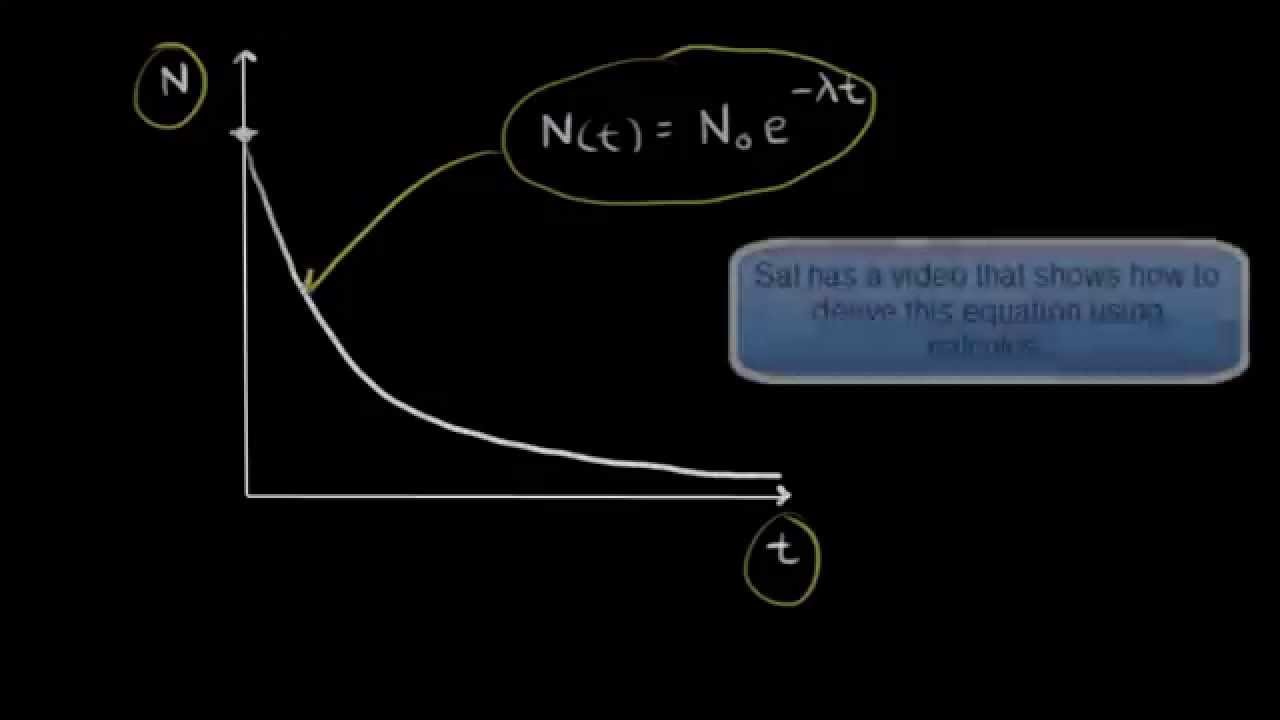
Tady vidíme graf exponenciálního rozpadu. N značí počet radioaktivních jader, jako funkci času. Takže tato rovnice popisuje náš graf. Tohle je počet radioaktiních jader v libovolném čase T, se rovná N s indexem nula... ...neboli počáteční počet jader... ...krát e na minus lambda krát t. Lambda je konstanta rozpadu. Takže tohle je konstantní číslo. Můžeme to pojmenovat 'k', pokud chceme, jakožto rychlostní konstantu. Ale je to určitá konstanta a teď ji vynásobíme časem. Řekněme, že chceme najít, co tenhle bod reprezentuje na našem grafu. To je právě když je čas nula. Dosaďme, že čas se rovná nula v této rovnici. Takže tohle je počet radioaktivních jader, ...když čas je nula, je toto rovno N₀, krát e na minus lambda krát t. Přičemž 't' je nula. Takže to je rovno N₀ krát e na nulu. Pokud umocním e na nultou, získám 1. Takže počet radioaktivních jader v čase nula, je rovno N₀. Tohle je N₀, počáteční počet radioaktivních jader na grafu. Toto můžeme udělat pro jakýkoliv čas 't'. Stačí si vybrat čas, řekněme že tohle je čas, který jsme vybrali, přesunout se sem nahoru a tím nalezneme, jaká hodnota je na tomto grafu. V libovolném čase 't' je tohle počet radioaktivních jader. Udělejme to pro poločas. Takže pamatujme, když poločas... ...když se čas rovná poločasu rozpadu, počet radioaktivních jader... ...tohle by bylo řekněme jeden poločas... ...takže tohle by bylo počáteční množství vydělené dvěma. Takže polovina zůstává. Podívejme se na graf, když vezmeme N₀, vydělíme to 2, výsledek je přibližně tady. Řekněme že tohle je N₀ lomeno 2. Přejdeme sem, a nalezneme náš čas, takže tohle bude náš poločas. Tenhle čas reprezentuje poločas. Tady je to znázorněno graficky. Vezmeme konkrétní čísla. Vezmeme poločas a počet radioaktivních jader a dosadíme to do naší rovnice. Dobře, udělejme to. Potřebuji trochu víc místa. Přepíšu rovnici tady. Máme počet radioaktivních jader jako funkce času se rovná počátečnímu počtu radioaktivních jader krát e na minus lambda 't'. Dosadíme to sem. Když mluvíme o poločase, dosadíme to tady za čas. A potom počet radioaktivních jader bude N₀ lomeno 2. Dosadíme. Dostáváme N₀ lomeno 2, se rovná N₀ krát e na minus lambda krát poločas. Vidíme, že lze vykrátit N₀. Na levé straně nám vychází polovina se rovná e na minus lamda krát poločas. Teď se zbavme exponenciely. Dáme přirozený logaritmus na obě strany. Tedy zlogaritmuji obě strany rovnice přirozeným logaritmem. Přirozený logaritmus z jedné poloviny se rovná přirozený logaritmus e na minus lambda 't polovina'. Na levé straně přirozený logaritmus poloviny je rovno -0,693. To stačí zadat do kalkulačky a dostanete mínus 0,693. Napravo nám zmizí logaritmus i 'e' a zůstane jen to, co bylo v exponentu. Takže teď tu máme minus lambda 't polovina'. Nemusíme se starat o to záporné znaménko, z tohoto zbyde jenom 0,693, a to je rovno lambda krát 't polovina'. Vyřešíme čemu se rovná poločas. Tedy, čemu se rovná 't polovina'. Takže 't polovina' je rovno 0,693 děleno lamba, neboli konstantou rozpadu. Takže tohle je jedna z těch rovnic, co vidíte pro poločas. Co když chceme vypočítat lambdu, konstantu rozpadu. Je to vlastně jednoduché. Vypočteme konstanta rozpadu se rovná 0,693 děleno poločas. Vidíme, že tu jen vyjadřuji různé neznámé z jedné rovnice. Můžeme vypočítat poločas nebo konstantu rozpadu. Můžeme jít tam a zpátky mezi poločasem a konstantou rozpadu. Když jedno známe, druhé dopočteme. Takže to byla úvaha o grafu exponenciální proměny. Ukažme si teď semilogaritmické znázornění, což je trochu jiný pohled na data. ...udělám si místo... Přepíšu sem původní rovnici. Ta nám říká, že počet radioaktivních jader se rovná počátečnímu počtu krát e na minus lambda 't'. Takže převedeme tohle, aby to byla rovná čára. Musíme vydělit N číslem N₀. Máme N lomeno N₀. Vydělíme obě strany číslem N₀ a dostaneme e na minus lambda 't'. Teď se zbavíme exponenciely. Stejně jako minule použijeme přirozený logaritmus. Dáme ho na obě strany, přirozený logaritmus N lomeno N₀ se rovná přirozenému logaritmu e na minus lambda 't'. Na levé straně mám logaritmus podílu, který můžu napsat jako rozdíl logaritmů. Přirozený logaritmus N lomeno N₀ je roven přirozenému logaritmu N minus přirozený logaritmus N₀ Napravo tohle odpadá a zůstane tohle. Takže minus lambda 't'. Napravo máme minus lambda 't'. Když to trochu upravím, Vyjádříme ln N, které je rovno minus lambda 't' navíc plus přirozený logaritmus N₀. A teď máme velmi zajímavou formu. Když se pozorně podíváme vidíme, že je to to samé jako 'y' rovná se mx plus b, což je rovnice pro přímku. Tedy 'y' zde představuje přirozený logaritmus N. 'm' odpovídá členu minus lambda. Co bude potom 't'? To odpovídá 'x'. A nakonec logaritmus N₀ se rovná 'b'. Takže 'y' se rovná mx plus b. To je rovnice přímky, kterou byste měli znát z matematiky. Ve které 'm' je směrnice. Takže směrnice v našem případě je minus lambda. Pamatujete si též, že tohle je průsečík s osou y? Člen 'b' tedy odpovídá průsečíku na ose y. Pokud bychom nakreslili graf naší zkoumané funkce, je to průsečík daný členem logaritmus z N₀. Pojďme to rychle zakreslit. Nebudu se zaobírat detaily, ale když to zakreslujeme... Pokud je tohle naše osa y... ...dám to do závorky protože to není co dělám... Tohle je naše osa x, podívejme se na to znovu. Pro moje y, dosadím do grafu přirozený logaritmus N. Použiju jinou barvu aby jsme to viděli. Přirozený logaritmus N bude na ose y a na ose x je čas. Čas máme tady. Víme, že průsečík s osou y je roven ln N₀. Takže průsečík s osou y bude někde tady označím to jako ln N₀. A můžeme to jednoduše dokázat. Když čas je nula, takže když čas je nula, dosadíme, máme tu přirozený logaritmus N, což je rovno minus lambda krát nula plus přirozený logaritmus N₀. Tohle půjde pryč a vidíme, že máme přirozený logaritmus N₀ rovno tomuto bodu. To je tedy náš průsečík s osou y. Víme, že je to graf rovné čáry. Máme negativní směrnici. Když to tedy nakreslím, bude to vypadat takhle, jen si představte, že je to přímka. Moc se mi to nepovedlo ale použijte představivost. A směrnice je... Co je to vlastně směrnice? Je to změna y lomeno změna x. To je změna na této ose lomeno změna na této. To je rovno minus lambda, o které jsme mluvili tady. Když uděláme semilogaritmické zobrazení, protože máme přirozený logaritmus tady versus tady. Dává nám to informaci, takže je to jiný pohled na data. Můžeme najít směrnici téhle rovné čáry, uděláme z ní negativní hodnotu a dostaneme konstantu rozpadu. A z konstanty rozpadu umíme dopočítat poločas. A znova, někdy uvidíme semilogaritmické grafy jako jiný pohled na data.

0:00
10:16