Nevychýlený odhad rozptylu (simulace) Další simulace dokazující, že máme dělit (n - 1), chceme-li získat nestranný odhad populačního rozptylu.

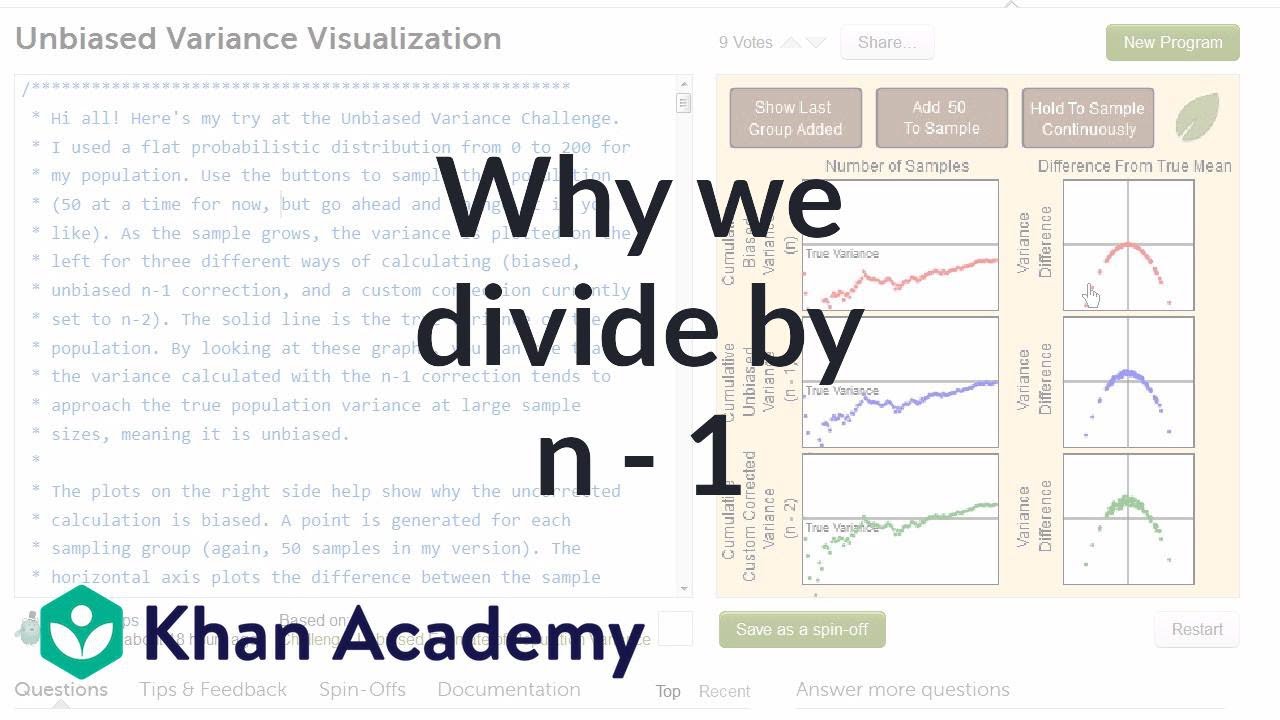
Tady je simulace, kterou vytvořil uživatel Khan Academy jménem Justin Helps. Ta se nám opět snaží ukázat, proč při výpočtu výběrového rozptylu dělíme výrazem (n - 1), když chceme získat nevychýlený odhad populačního rozptylu. Máme tady populaci, která má rovnoměrné rozdělení. Populace má rovnoměrné rozdělení na intervalu 0 až 200. Budeme dělat výběry z této populace o velikosti 50. V každém z těchto výběrů spočítáme výběrový rozptyl a budeme přitom dělit n. a pak pro srovnání budeme dělit výrazem (n - 1) a pak (n - 2). A jak se bude počet výběrů zvětšovat, zprůměrujeme rozptyly spočítané těmito různými způsoby. A zjistíme, k čemu tyto průměru konvergují. Takže tady máme jeden výběr, další výběr, další výběr. Budu postupně přidávat další a další výběry. A vidíte, že se tu začíná dít něco zajímavého. Když dělíme výrazem n, tak i když mám velkou spoustu výběrů, stále podhodnocuji skutečný roztpyl. Zatímco když dělím výrazem (n - 1), dostanu docela dobrý odhad. Průměr všech výběrových rozptylů konverguje ke skutečnému rozptylu. Když dělím výrazem (n - 2), je zřejmé, že v průměru nadhodnocuji spočtený výběrový rozptyl proti skutečnému rozptylu. Takže díky tomu vidíme, že je nejlepší dělit výrazem (n - 1). Na těchto grafech vidíme totéž jinak. Každý bod představuje jeden výběr. Na horizontální ose je zachyceno, o kolik větší či menší je výběrový průměr proti skutečnému průměru. Takže například v tomto výběru napravo je výběrový průměr o hodně větší než skutečný průměr. V tomto výběru nalevo byl výběrový průměr naopak o mnoho menší než skutečný. A tady byl výběrový průměr jen nepaterně větší než skutečný. Na vertikální ose srovnáváme rozptyl spočítaný dvěma způsoby: s použitím výběrového průměru a skutečného průměru. A dělíme v tomto případě vždy výrazem n. Na svislé ose pak porovnáváme rozdíl mezi průměrem spočítaným s využitím výběrového a populačního průměru. Takže například tady spočítáme průměr pomocí výběrového průměru, což normálně děláme. A vidíme, že dost podhodnocujeme skutečný průměr, který ovšem většinou neznáme. A když to všechno spočítáte, dostanete tento zajímavý tvar. Zamyslete se nad tím, jak koneckonců tvůrce aplikace doporučuje. Proč tu vznikl takový tvar? Další důležitá věc: vidíme, že celý graf je pod vodorovnou osou. Takže když používáme při výpočtu rozptylu výběrový průměr, což obvykle děláme, tak vždycky podhodnocujeme. Vždycky dostaneme menší rozptyl, než kdybychom použili populační průměr. Když však dělíme výrazem (n - 1), nedojde k podhodnocení vždy. Někdy naopak nadhodnocujeme. Avšak když všechny tyto rozptyly zprůměrujeme, budou konvergovat ke skutečnému rozptylu. A tady nadhodnocujeme o něco více. Proberu to trochu podrobněji. abychom měli jasno v tom, co na těchto grafech vidíme. Abychom si to ujasnili: na tomto červeném grafu... zkusím použít nějakou podobnou barvu. V každém z těchto výběru počítám výběrový rozpyl s použitím výběrového průměru a dělíme přitom n. Od toho odečteme výběrový rozptyl, nebo to nazvěme pseudo-výběrový rozptyl, spočtený za předpokladu, že odněkud známe populační průměr. Ale to není zrovna běžný případ. Ale ukážeme si tak, jak moc tím dojde k podhodnocení výběrového rozptylu ve srovnání se situací, kdy máme k dispozici populační průměr. Počítáme rozdíl mezi takto spočtenými výběrovými rozptyly. Vidíte, že to podhodnotíme vždycky. Tady trochu nadhodnocujeme, ale někdy taky podhodnocujeme. A když to zprůměrujeme přes všechny výběry, bude to konvergovat ke skutečnému rozptylu. Tady děláme totéž, ale dělíme (n - 1) a (n - 2).