Úvod do rozdělení chí-kvadrát Co je to rozdělení chí-kvadrát?

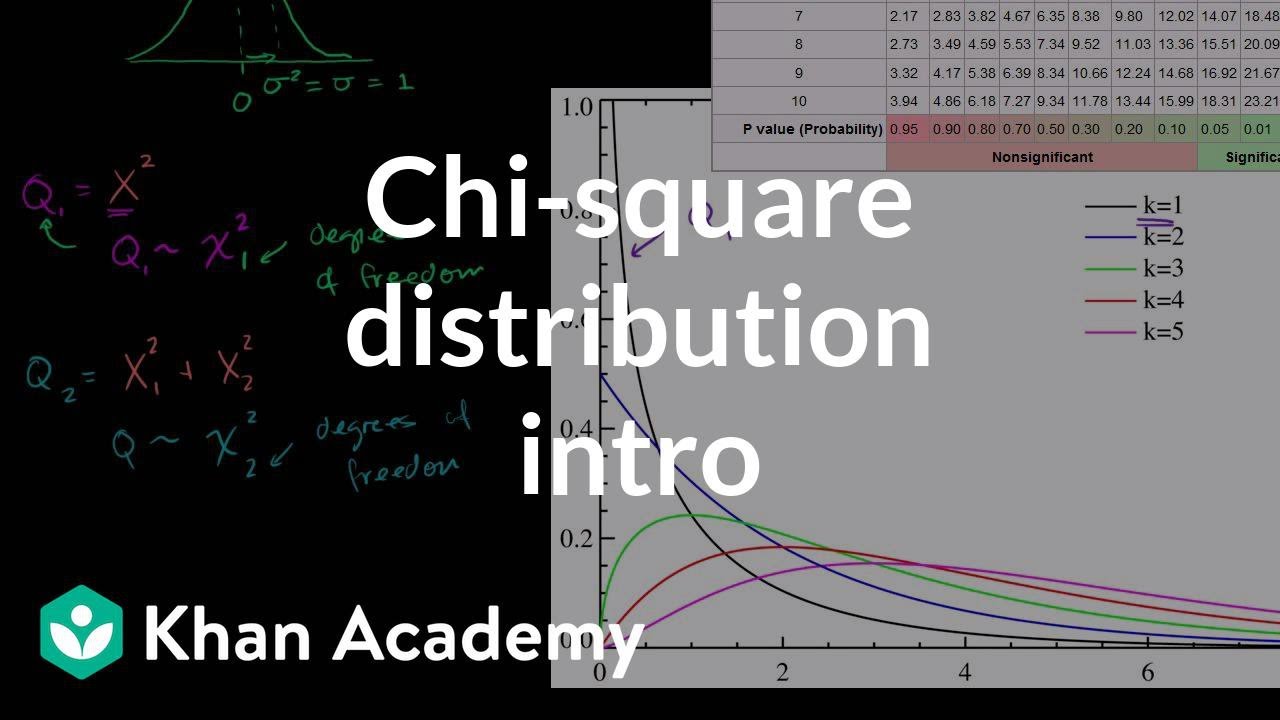
V tomto videu si povíme o tom, co je to rozdělení chí-kvadrát. A v několika dalších videích jej skutečně použijeme, když budeme chtít testovat, jak se teoretická rozdělení liší od napozorovaných, nebo jak dobře odpovídají napozorovaná data teoretickému rozdělení. Takže se nad tím trochu zamysleme, řekněme, že máme nějaké náhodné veličiny. A pro každou z nich platí, že je to nezávislá veličina z normálního rozdělení. Připomeňme si, co to znamená, řekněme, že máme náhodnou veličinu X. Jestliže je X normálně rozdělená veličina, můžeme psát, že X je náhodná veličina z normálního rozdělení s průměrem 0 a rozptylem 1. Jinak řečeno, střední očekávaná hodnota X je rovna 0 a rozptyl naší náhodné veličiny X je roven 1. Abychom si to lépe představili, pokud náhodně vybereme jednu hodnotu X, provádíme náhodný výběr z normovaného normálního rozdělení, které vypadá takto. Průměr je 0 a rozptyl je 1, což by také znamenalo, že směrodatná odchylka je rovna 1. Takže tohle by mohlo být normované normální rozdělení. Jeho rozptyl i směrodatná odchylka by se rovnaly 1. Takže rozdělení chí-kvadrát... Pokud vezmeme pouze jednu z těchto náhodných veličin... definujme si novou náhodnou veličinu, náhodnou veličinu Q, kterou získáme tak, že provedeme náhodný výběr veličiny X z tohoto normovaného normálního rozdělení a toto číslo umocníme na druhou. Takže Q se rovná této náhodné veličině X umocněné na druhou. Rozdělené této náhodné veličiny bude příkladem rozdělení chí-kvadrát. V tomto videu uvidíme, že rozdělení chí-kvadrát je ve skutečnosti skupina rozdělení, které závisí na tom, kolik takových náhodných veličin sčítáme. Nyní máme pouze jednu náhodnou veličinu, s jejíž druhou mocninou pracujeme, což je pouze jednou z možností, o dalších si povíme za chviličku. Můžeme tedy psát, že Q je náhodná veličina z rozdělení chí-kvadrát, nebo bychom to mohli napsat takto: toto už není X, jde o řecké písmeno chí, ačkoli to vypadá trochu jako pokroucené X. Je to tedy příklad rozdělení chí-kvadrát, a protože vychází z druhé mocniny pouze jednoho čísla, sčítáme totiž pouze jednu nezávislou náhodnou veličinu z normovaného normálního rozdělení, tak říkáme, že toto výsledné rozdělení má jeden stupeň volnosti, a napíšeme to sem, toto je označení počtu stupňů volnosti. Máme nyní jeden stupeň volnosti. Definujme si tuto veličinu jako Q1 a řekneme, že máme jinou náhodnou veličinu, nazvěme ji Q2. Potřebujeme jinou barvu... nakreslíme si to třeba modře. Máme jinou náhodnou veličinu Q2, která vznikne takto: máme jednu náhodnou normálně rozdělenou veličinu, nazvěme ji X1, umocníme ji na druhou, a vezmeme další nezávislou normálně rozdělenou veličinu X2, kterou také umocníme. Obě takto vzniklé náhodné veličiny mají podobná rozdělení a obě jsou nezávislé. Abychom získali Q2, tak stačí provést náhodný výběr veličiny X1 z tohoto rozdělení, umocnit tuto veličinu na druhou, provést další náhodný výběr jiné veličiny X2 z téhož rozdělení, také ji umocnit na druhou, a pak jejich druhé mocniny sečíst. Tak dostaneme Q2. A napíšeme, že Q2 je náhodná veličina z rozdělení chí-kvadrát se dvěma stupni volnosti. Abychom si lépe představili, jak vypadají rozdělení chí-kvadrát, podívejme se na chvíli sem. Tohle mám z wikipedie, ukazuje to hustoty pravděpodobnosti rozdělení chí-kvadrát. Tohle první má jeden stupeň volnosti, což odpovídá naší veličině Q1. Tohle je funkce hustoty pravděpodobnosti pro Q1 a vrchol má blízko nule, což dává smysl. Pokud provádíme náhodný výběr z normovaného normálního rozdělení, existuje velká pravděpodobnost, že vybereme číslo blízké nule. A pokud umocníme číslo blízké nule na druhou, výsledek bude méně než jedna, velmi blízko nule, takže existuje vysoká pravděpodobnost, že výsledná hodnota bude menší než určitý práh, v tomto případě jedna, zároveň existuje poměrně malá pravděpodobnost, že výsledná hodnota bude velké číslo. Abychom získali hodnotu 4, museli bychom vybrat číslo 2 z tohoto rozdělení, a jak víme, číslo 2 odpovídá dvěma směrodatným odchylkám od průměru, je tedy méně pravděpodobné, že jej vybereme, a ještě méně pravděpodobné, že vybereme dokonce větší číslo. Proto má rozdělení chí-kvadrát právě tento tvar. Když máme 2 stupně volnosti, tvar výsledného rozdělení je méně extrémní, tato modrá čára odpovídá tvaru rozdělení Q2, přičemž vidíme, že je o něco méně pravděpodobné získat hodnoty blízké 0. A o něco pravděpodobnější získat vzdálenější hodnoty, ale stále je toto výsledné rozdělení sešikmené směrem k malým hodnotám. Pokud bychom přidali další náhodnou veličinu, nazvěme ji Q3, kterou bychom definovali jako součet tří druhých mocnin nezávislých náhodných veličin z normovaného normálního rozdělení, tedy X1 na druhou plus X2 na druhou plus X3 na druhou, tak bychom získali naše Q3, neboli náhodnou veličinu z rozdělení chí-kvadrát se třemi stupni volnosti, čemuž odpovídá tato zelená čára. Možná jsem měl toto napsat zeleně, jde o tuto zelenou čáru a všimněme si, že máme opět vyšší pravděpodobnost, že získáme tyto vyšší hodnoty. Je to proto, že ačkoli každá ze sčítaných hodnot může být velmi malá, jejich součet již tak malý nebude, proto se rozdělení začíná stáčet doprava. Čím více máme stupňů volnosti, tím méně bude rozdělení sešikmené směrem nalevo, tím více bude naopak symetrické. Co je na rozdělení chí-kvadrát zajímavé, a čím se myslím liší od jakéhokoli jiného rozdělení, které jsme dosud poznali, je, že neobsahuje hodnoty nižší než 0, protože jde o součet druhých mocnin, a i když výchozí náhodné veličiny mohou být záporné, jelikož pochází z normálního rozdělení, jejich druhé mocniny již budou kladné, a jejich součet bude tudíž vždy kladným číslem. Jak uvidíme v dalších videích, toto rozdělení bude užitečné pro zjišťování chyby nebo odchylky od očekávané hodnoty. Spočítáme-li celkovou chybu, můžeme zjistit pravděpodobnost této chyby. Neboli rozdíl mezi skutečnými hodnotami a předpokládanými parametry. O tom si povíme v dalším videu. Ještě vám chci ale ukázat, jak číst tabulky rozdělení chí-kvadrát. Pokud bych se vás zeptal... předpokládejme, že tohle je naše rozdělení, vybereme si třeba tohle modré, které má dva stupně volnosti, protože vzniklo součtem dvou veličin. Pokud bych se vás zeptal, jaká je pravděpodobnost, že Q2 je větší než určitá hodnota... řeknu to takhle: jaká je pravděpodobnost, že Q2 je větší než 2,41? Tuto hodnotu vybírám úmyslně. Chci zjistit pravděpodobnost, že Q2 je větší než 2,41. Co potřebuji udělat, je toto: podívám se do tabulky rozdělení chí-kvadrát, Q2 je rozdělení chí-kvadrát s dvěma stupni volnosti, proto se podívám sem do řádku s dvěma stupni volnosti, a chci znát pravděpodobnost, že dostanu hodnotu vyšší než 2,41. A zvolil jsem 2,41 proto, že se skutečně nachází v této tabulce. Důvod, proč tabulka obsahuje tato divná čísla místo celých čísel nebo snadných zlomků, vychází z p-hodnot, tedy z pravděpodobností, že získáme číslo větší než tato hodnota. Většinou na to jdeme obráceně, ptáme se, pro jakou hodnotu platí, že máme 30% pravděpodobnost získání něčeho většího než tato hodnota. Pak bychom zjistili, že jde o hodnotu 2,41. Ale my to pro účely tohoto videa děláme naopak. Chceme zjistit pravděpodobnost, že náhodná veličina bude větší než 2,41. Tady si přečteme, že je to 30 %. Pokud se podíváme na graf, zjistíme, že číslo 2,41 se bude nacházet... moment, tohle je 3, tohle 2,5, takže 2,41 bude někde tady. Tabulka nám tedy říká, že tato oblast pod modrou křivkou, co je to? Tato oblast napravo bude 30 %. Respektive 0,3. Můžeme na to nahlížet jako na 30% celkové plochy pod křivkou, jelikož všechny pravděpodobnosti samozřejmě dávají součet 1. Toto byl tedy úvod do rozdělení chí-kvadrát. V příštím videu jej skutečně použijeme k testování některých hypotéz.