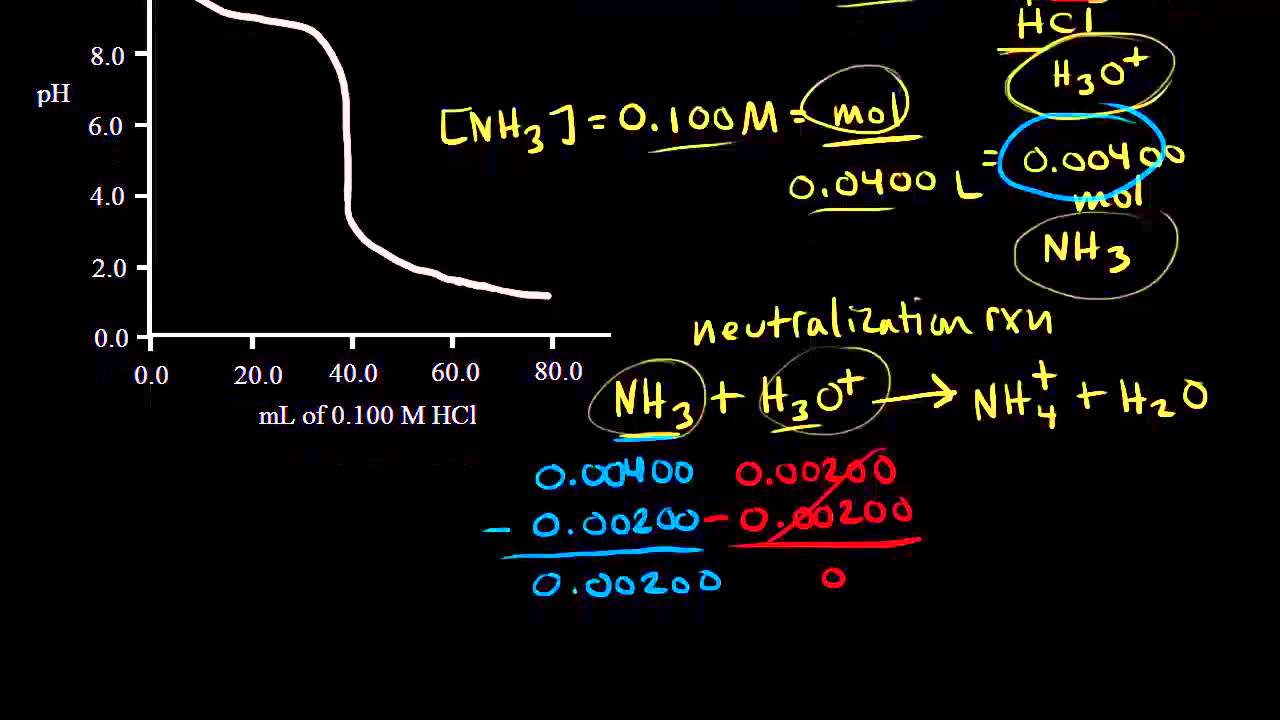
Titrace slabé zásady silnou kyselinou 1 V této sérii dvou videí si ukážeme a vypočítáme titrační křivku pro titraci slabé zásady silnou kyselinou. V první části si ukážeme, jak vypočítat pH před přidáním kyseliny a v bodě poloviční ekvivalence.