Poločas reakce druhého řádu V návaznosti na předcházející video si teď odvodíme vztah pro výpočet poločasu reakce druhého řádu, který již není konstantou.

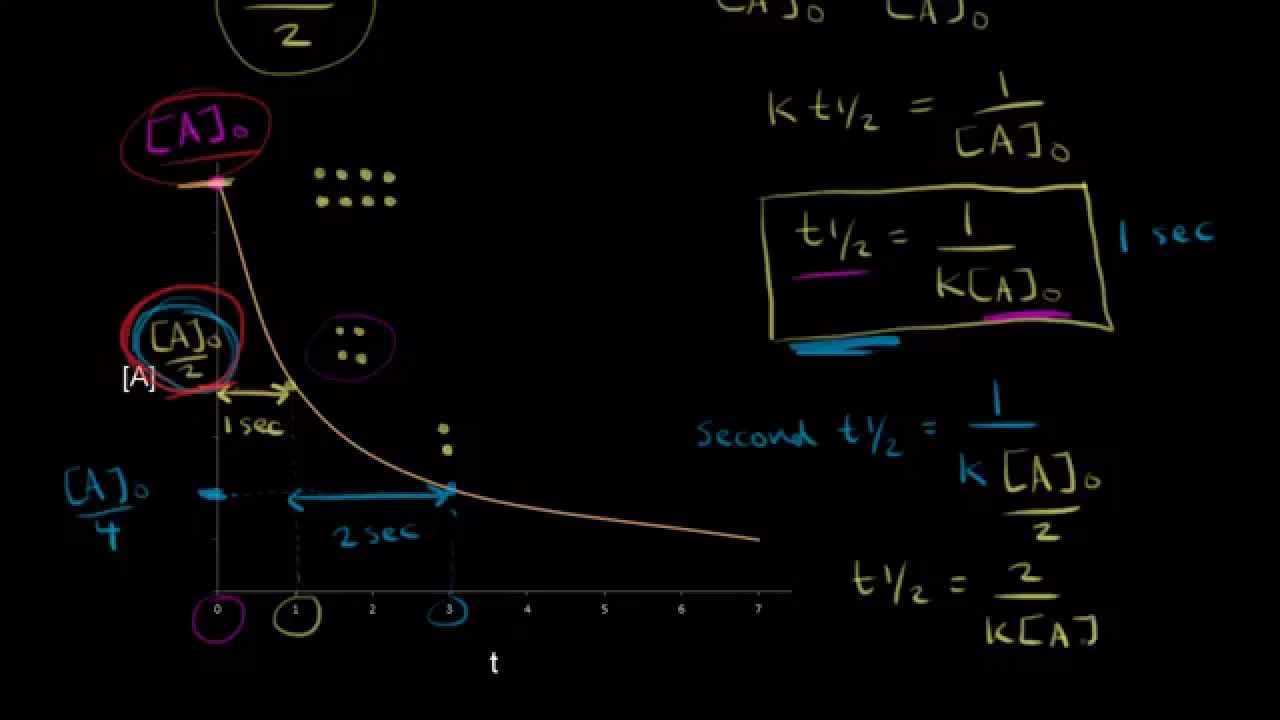
Už jsme o definici poločasu rozpadu mluvili. Připomínám, že se poločas rozpadu značí t(1/2) Poločas rozpadu je čas, během kterého koncentrace dané látky klesne na polovinu původní koncentrace. Už jsme také mluvili o rychlostním vzorci nebo o rychlostní rovnici pro reakce druhého řádu. Tohle je jeden ze zápisů. 1 lomeno koncentrace látky A minus 1 lomeno počáteční koncentrace látky A se rovná rychlostní konstantě 'k' krát čas. Takže pokud se bavíme o poločasu rozpadu, takže když čas je roven poločasu rozpadu, takže dosadíme t(1/2) za čas. Jaká je koncentrace látky A? Známe definici poločasu rozpadu, takže koncentrace látky A by měla být poloviční oproti původní koncentraci. Takže naše původní koncentrace je tohle. Takže to je polovina z původní koncentrace. Tak to sem dosadíme. Dobře, dosadíme to sem a uvidíme, co nám vznikne. Máme 1 lomeno původní koncentrace látky A dělená 2 minus 1 lomeno původní koncentrace látky A se rovná rychlostní konstantě 'k' krát poločas rozpadu. Takže na levé straně to prostě bude 2 lomeno původní koncentrace látky A minus 1 lomeno původní koncentrace látky A se rovná 'k' krát poločas rozpadu. Kolik je tedy 2 lomeno původní koncentrace látky A minus 1 lomeno původní koncentrace látky A? To je prostě 1 lomeno původní koncentrace látky A, a to se rovná rychlostní konstantě 'k' krát poločas rozpadu. Teď můžeme spočítat poločas rozpadu. Prostě obě strany vydělíme 'k'. Takže nám vychází, že poločas rozpadu je roven 1 lomeno 'k' krát původní koncentrace látky A. A tady máme rovnici pro poločas rozpadu u reakce druhého řádu. Všimněte si, že vypadá jinak než u poločasu rozpadu pro reakce prvního řádu. U reakcí prvniho řádu jsme viděli, že poločas rozpadu byla konstanta, ale tady poločas rozpadu není konstanta, protože poločas rozpadu je závislý na počáteční koncentraci látky A. Podívejme se na graf závislosti koncentrace na čase pro reakce druhého řádu, abychom to trochu lépe pochopili. Takže pokud čas je 0, tento bod na grafu bude původní koncentrace látky A. Takže tady je naše původní koncentrace látky A. A představme si průběh té reakce. Řekněme, že začínáme s 8 částicemi, s 8 molekulami, takže tady máme jedna, dva, tři, čtyři, pět, šest, sedm, osm. Dobře, takže když počkáme až koncentrace klesne na polovinu z té původní, co nám zbyde? Zbydou nám 4 molekuly. Dobře, zbydou nám 4 molekuly, tak je sem namaluju a jak dlouho trvalo než z 8 byly 4? No, vidíme to na grafu. Pokud tenhle bod je počáteční koncentrace, polovina bude přímo tady. Což je počáteční koncentrace látky A dělená 2. Takže ten bod najdeme na grafu a najdeme ho zde na ose x a vyšla nám jedna sekunda. Takže náš první poločas rozpadu je jedna sekunda. Tak to sem napíšu. Tohle je první poločas rozpadu, což je jedna sekunda. Jak dlouhý je druhý poločas rozpadu ? Jak dlouho trvá než to snižíme počet molekul za 4 na 2 molekuly? ...jen si změním barvu ať se v tom vyznáme... Takže jdeme ze 4 molekul na 2 molekuly. Jak dlouho to potrvá? No, pokud tohle je teď naše počáteční koncentrace, kolik je polovina? Tak, na našem grafu to je přímo zde. A zároveň to je počáteční koncentrace dělená teď už čtyřmi. Tady máme polovinu tohohle, a když půjdeme sem najdeme ten bod na našem grafu, že? Takže ten bod na našem grafu bude tady a dolů na osu x a vidíme, že čas je 3. Takže jak dlouhý je poločas rozpadu tentokrát ? Tentokrát náš poločas rozpadu jsou 2 sekundy. Že? Poločas tohoto rozpadu jsou 2 sekundy. Což je dvakrát tolik co první poločas rozpadu a můžeme pochopit, proč, dosazením za poločas rozpadu do naší rovnice zde. Když první poločas rozpadu je 1 sekunda, takže první poločas rozpadu je 1 sekunda, jdeme dál a dosadíme sem druhý poločas rozpadu. Takže druhý, druhý poločas rozpadu se rovná, to bude 1 lomeno rychlostní konstanta k ale teď počáteční koncentrace... ...počáteční koncentrace není tohle, že? Je to tohle. Je to počáteční koncentrace dělená dvěma. Takže zpátky sem, tohle bude počáteční koncentrace látky A dělená 2. Takže pro druhý poločas rozpadu to bude 2 lomeno 'k' krát počáteční koncentrace látky A. A vidíme, že tohle je dvakrát víc než tohle zde. Když tohle je první poločas rozpadu, tak tohle dvojnásobek toho, což jsou samozřejmě 2 sekundy. Což dává smysl, jak podle grafu, tak i podle rovnice pro poločas rozpadu. Takže náš druhý poločas rozpadu je dvakrát tak dlouhý než ten první. A každý další poločas rozpadu bude dvakrát tak dlouhý než ten předchozí. Takže když počkáme ještě jeden poločas rozpadu, na třetí, půjdeme ze 2 molekul na 1 molekulu. Počáteční koncentrace teď bude tohle. Kolik je potom polovina? To bude tady, takže jdeme sem a najdeme ten bod na našem grafu. Takže najdeme ten bod tady na grafu a dolů na osu x a vidíme, že čas je roven 7 sekundám. Takže kolik je třetí poločas rozpadu? Tohle je ten třetí poločas rozpadu a to jsou samozřejmě 4 sekundy, že? Takže 4 sekundy, což je dvojnásobek předešlého poločasu rozpadu. Dobře, koukneme se, jestli z toho ještě něco vydedukujeme. Takže co to znamená? To znamená, že v brzké fázi naší reakce máme vyšší koncentraci látky, že? A vyšší koncentrace znamená, že ty molekuly tam do sebe můžou lépe narážet a tím pádem reakce probíhá rychleji, takže pokud máme vyšší koncentraci, máme vyšší reakční rychlost. Tím pádem čím rychleji se látka spotřebovává, a tím pádem čím kratší poločas rozpadu, tím kratší dobu trvá než koncentrace látky klesne na polovinu počáteční koncentrace.