Reakční kinetika (14/19) · 9:53
Reakce nultého řádu Dozvíme se, co znamená, že reakce probíhá dle kinetiky prvního řádu a ukážeme si, jak vypočítat její poločas rozpadu.
Pojďme se podívat na reakci nultého řádu. Látka A se zde promění na produkty. V čase nula máme danou počáteční koncentraci A₀. V čase 't' již máme jinou koncentraci, A s dolním indexem t. Z tohoto dokážeme popsat rychlost reakce. Jeden ze způsobů, jak jí vyjádřit, je vzpomenout si na vzoreček. Rychlost reakce je rovna záporně vzaté změně koncentrace lomená změnou v čase. Také bychom si rychlost mohli vyjádřit z rychlostní reakce. Dle té je rychlost reakce rovna rychlostní konstantě 'k' krát koncentrace složky A. A protože jsem řekl, že tato reakce je nultého řádu, tak koncentraci látky A umocním na nultou. A jakékoliv číslo na nultou je rovno jedné. Proto se rychlost reakce rovná 'k' krát 1. To znamená, že rychlost reakce je rovna rychlostní konstantě 'k'. Takže rychlost reakce nultého řádu je konstantní. Je nezávislá na koncentraci A. Když tyto dvě rovnice spojíme, vyjde nám: k je rovno negativní změně v koncentraci A děleno změnou v čase. Tak nám vznikla rovnice, kde negativní změna koncentrace A podělená změnou času, je rovna rychlostní konstantě 'k'. Jak vypočítáme tuto diferenciální rovnici? Máme tu malou změnu v koncentraci lomenou změnou času. Napíšeme to jako rychlost změny koncentrace v závislosti na čase. Tady máme minus a pak máme 'k' na pravé straně Takže jsem připraveni přemýšlet o naší diferenciální rovnici. Celou rovnici vynásobíme členem '-dt'. Tím dostáváme, že změna koncentrace A je rovna minus k krát změna v čase 'dt'. A nyní můžeme integrovat. Zintegrujeme levou stranu, 'k' je konstanta, takže ji můžeme dát před integrál vpravo. Pojďme se podívat na začátek, abychom zjistili, v jakých mezích budeme integrovat. Bude to od času 0 až do nějakého času 't'. Druhý integrál bude od počáteční koncentrace A₀ do koncentrace po uplynutí času 't', kterou označujeme A. Tedy integrál vpravo bude od nuly do času 't' a integrál vlevo bude od počáteční koncentrace do koncentrace v čase 't'. Vidíme, že tu máme dva jednoduché integrály. Čemu se rovná integrál z dA? Mělo by to být samozřejmě A, tím myslím koncentrace A. Dobře, takže máme koncentraci A. Zde ještě musíme dosadit meze, tedy koncentrace A v čase 0 a 't'. Napravo máme další určitý integrál Integrál z dt. Výsledkem je 't'. Vyjde nám tedy minus k krát t v mezích od 0 do 't'. Dle základního principu výpočtu určitého integrálu nám na levé straně vyjde A minus A₀. A to se rovná minus k krát t. A toto je rychlostní rovnice v integrovaném tvaru pro reakce nultého řádu. Ještě bychom to měli upravit. Přesuneme počáteční koncentraci na pravou stranu takže naše konečná koncentrace je rovna zápornému k krát t plus počáteční koncentraci A₀. A toto je jiný způsob zápisu rychlostní rovnice v integrovaném tvaru. Odvodili jsme si rychlostní rovnici pro reakci nultého řádu A pokud se podíváme na tento tvar, připomíná nám rovnici přímky, kde y se rovná m krát x plus b. Když na x-ovou osu vyneseme čas, tak na ose y budeme mít aktuální koncentraci látky A. Tak nám vznikne přímka, a sklon této přímky určíme pomocí 'm', které se rovná zápornému 'k'. Takže sklon přímky určuje záporně vzatá rychlostní konstanta, což se taky odráží na počáteční koncentraci A. Nakreslíme si tady rychle graf. Podívejme se na spodní osu. Na této ose x budeme mít čas, takto označíme x-ovou osu. Na ose y budeme mít koncentraci látky A. Takže pojďme udělat přímku. Přepnu si to tu na kreslení přímek... Takže dostaneme takovouto přímku. Dobře. A toto je sklon přímky Sklon by měl být roven zápornému 'k'. Takže ještě jednou se na to můžeme podívat tady nahoře kde sklon je roven zápornému k. Tedy 'm' je rovno minus 'k'. Průsečík s osou y samozřejmě zobrazuje počáteční koncentraci. Tady vidíme počáteční koncentraci A. Takže toto je rychlostní rovnice v integrovaném tvaru pro reakce nultého řádu. Dále se pojďme podívat na poločas rozpadu. Je to čas, za který se koncentrace reaktantu sníží na polovinu z počáteční koncentrace. Takže když je čas roven poločasu rozpadu ...značíme jako t s indexem 1/2... Tedy když to dosadíme za 't', koncentrace A by měla být poloviční oproti počáteční koncentraci. Takže tu počáteční koncentraci vydělíme dvěma. Tento výraz dosadíme sem. Teď přepišme, co už máme. Teď máme počáteční koncentraci vydělenou dvěma, která se rovná minus k krát poločas rozpadu plus počáteční koncentrace A. Pojďme to vyjádřit pro poločas rozpadu. Na levé straně máme počáteční koncentraci A vydělenou dvěma neboli polovinu počáteční koncentrace A. Na pravé straně máme počáteční koncentraci A. Po úpravě to bude 1/2 minus 1. Což je minus 1/2. Tedy minus 1/2 krát počáteční koncentrace je rovna minus k krát t s indexem 1/2. Z toho si můžeme vyjádřit vzorec pro poločas rozpadu. Tedy t s indexem 1/2 je rovno počáteční koncentraci A děleno (2 krát k). Dvakrát rychlostní konstanta. Takto tedy můžeme vypočítat poločas reakce pro reakci nultého řádu. Uvědomme si, jak se změní poločas rozpadu, když zvýšíme počáteční koncentraci A₀. Je to přímá úměra. Takže pokud zvýším počáteční koncentraci A, tak se zvýší i poločas rozpadu. Takže by se měl poločas rozpadu zvyšovat Pojďme se podívat na příklad na reakci nultého řádu To nám pomůže trochu lépe porozumět poločasu rozpadu. Například reakce rozkladu amoniaku. Takže rozkladem amoniaku vzniká dusík a vodík. A tato reakce probíhá na povrchu kovového katalyzátoru. Jako katalyzátor používáme platinu. Tady nalevo nakreslím kousek platiny. Představte si tady povrch platiny a na povrchu platiny se vyskytují molekuly amoniaku, které s tímto povrchem přijdou do kontaktu. Nechte mě nakreslit modrou molekulu amoniaku, která přijde do kontaktu s povrchem platiny. Připomeňte si, že toto je reakce nultého řádu. Takže rychlost je rovna rychlostní konstantě krát koncentrace amoniaku na nultou. Takže zvýšení koncentrace amoniaku nemá efekt na rychlost. A tento obrázek nám tomu pomůže trochu lépe porozumět. Pokud zvýšíme koncentraci amoniaku tak, že přidám molekuly amoniaku, tak tím neovlivňuji celkovou rychlost reakce, protože molekuly amoniaku, které přidáme, nejsou v kontaktu s povrchem platiny. Takže jenom ty v kontaktu s povrchem mohou reagovat. Takže my zvýšíme koncentraci amoniaku, ale nemá to žádný efekt na rychlost, protože rychlost je limitovaná tím, jak velký má povrch náš kov. Takže byla situace číslo 1. Pojďme o tom přemýšlet ještě jinak. Máme náš povrch platiny. Nakreslím několik molekul amoniaku. Takže máme nějake molekuly v kontaktu s povrchem platiny a pak tu máme mnohem více dalších. Máme mnohem více molekul amoniaku a zřejmě velká část z nich se nedotýká povrchu našeho kovového katalyzátoru. Takže zvýšíme počáteční koncentraci látky A, samozřejmě látka A je v tomto případě amoniak. Poločas rozpadu se ale zvýší. To už víme z dřívějška. Pokud zvýšíme počáteční koncentraci A, tak dostaneme delší poločas rozpadu. A to dává smysl, protože naše reakce má konstantní rychlost, takže když tam máme náhle více molekul, tak zreagování poloviny z nich trvá déle. Takže máme všechny ty molekuly amoniaku, které se nedotýkají povrchu kovu, a tím je limitovaná naše rychlostní konstanta. Proto to trvá déle, neboť musí spotřebovávat polovinu modrých molekul v situaci číslo dva. Takže v porovnání situace číslo jedna a situace číslo dva, máme zvýšenou počáteční koncentraci A, a proto máme delší poločas rozpadu.
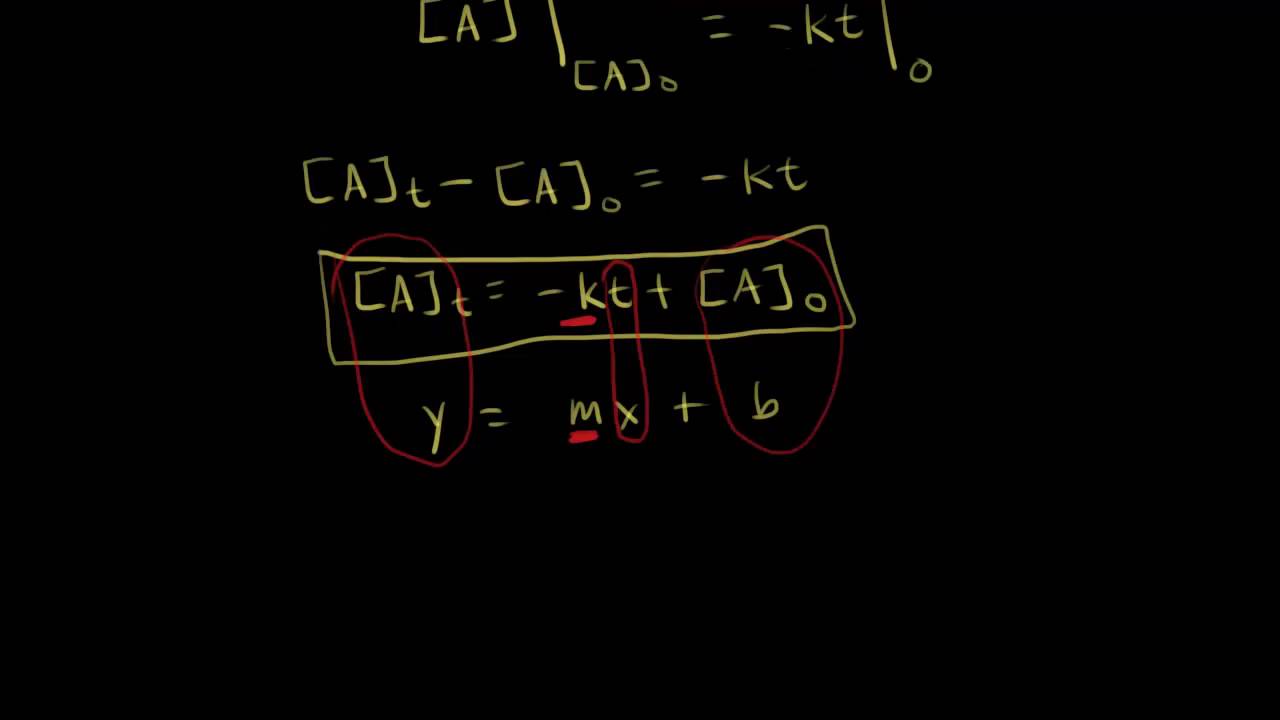
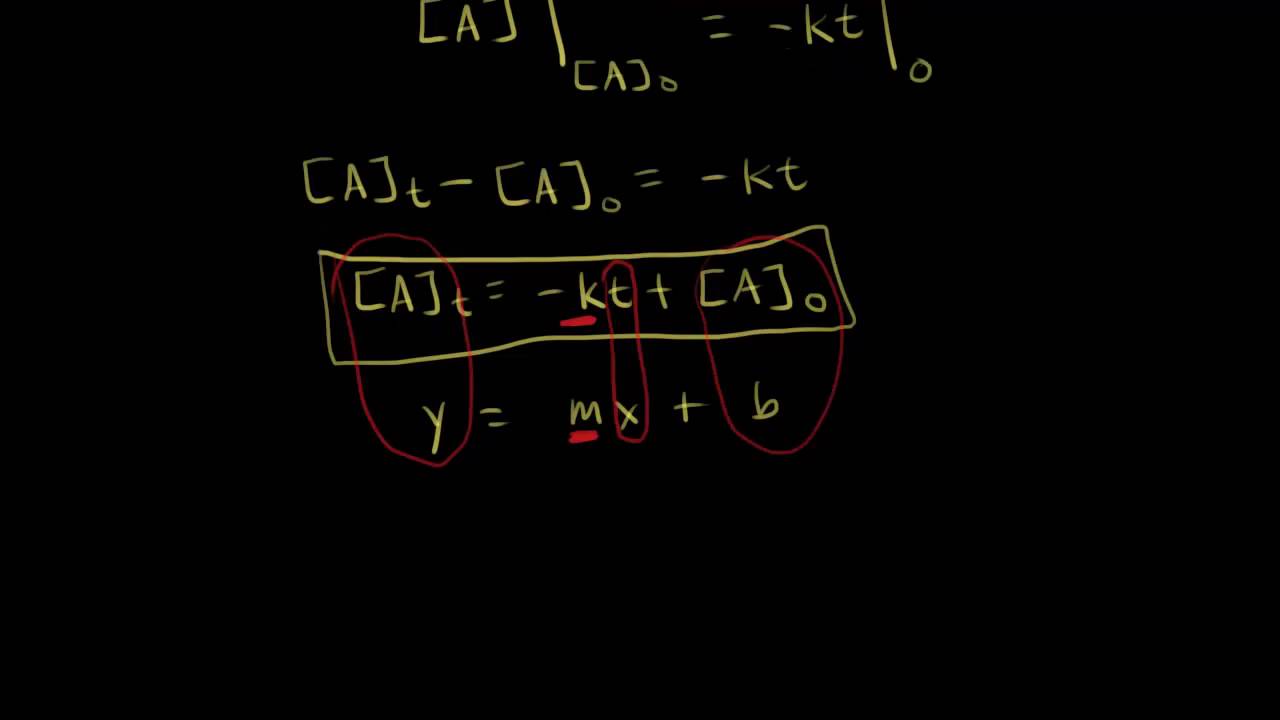
0:00
9:53