Reakční kinetika (18/19) · 11:06
Využití Arrheniovy rovnice Jak vypočítat aktivační energii reakce s využitím Arrheniovy rovnice?
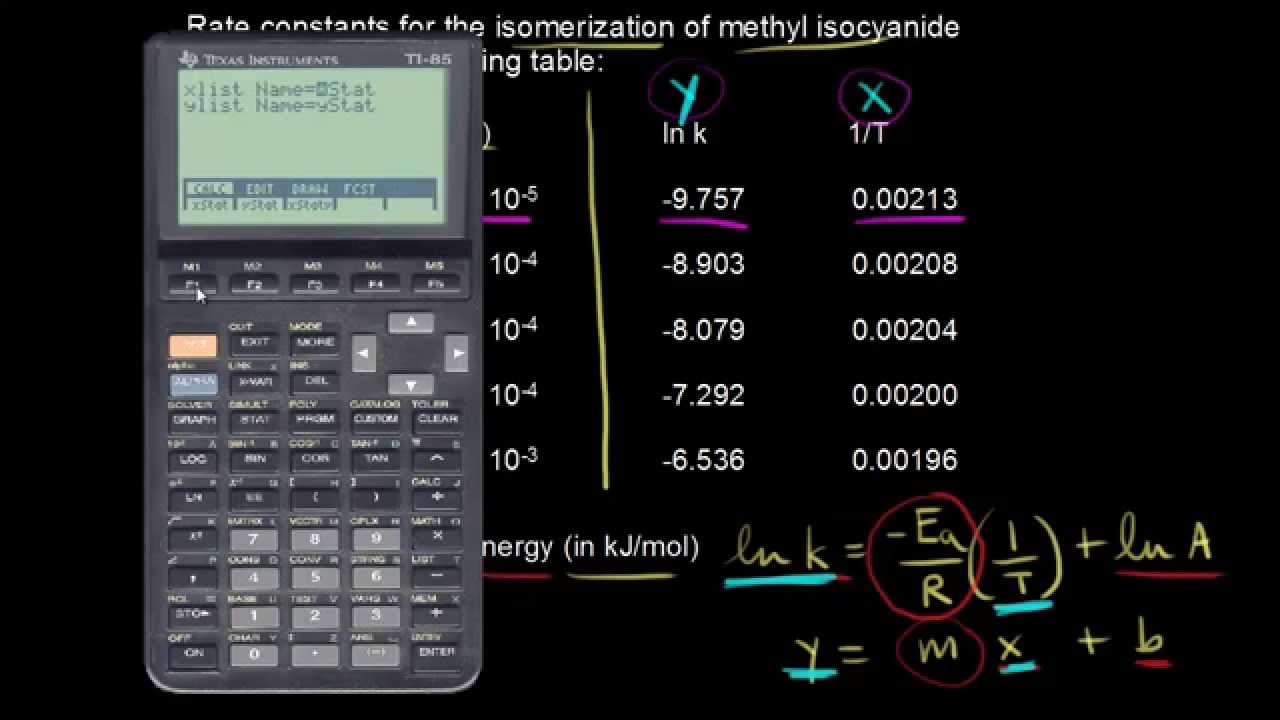
Jak můžeme využít Arrheniovu rovnici k nalezení aktivační energie reakce? Naše reakce je izomerizace methyisokyanidu. Vlevo tedy máme methyisokyanid a ten se přemění na svůj izomer, který máme na straně produktů. Je to reakce prvního řádu a tady máme různé rychlostní kontanty pro tuto reakci při různých teplotách. Řekněme, že zatím nemáme nic napravo od té čáry, kterou jsem teď nakreslil. Máme pouze rychlostní konstanty při různých teplotách. A v části a) po nás chtějí najít aktivační energii reakce v kJ na mol. Jedna možnost je vzpomenout si na jeden tvar Arrheniovy rovnice, o které bylo předchozí video. Byl to přirozený logaritmus rychlostní konstanty k se rovná –Ea lomeno R, kde Ea je aktivanční energie a R je plynová konstanta, krát 1 lomeno teplota plus přirozený logaritmus A, což je frekvenční faktor. A to je ta forma y se rovná mx plus b, že? y se rovná mx plus b. Pokud zakreslíte do grafu přirozený logaritmus rychlostní konstanty na ose y a 1 lomeno teplota na ose x, dostanete přímku. A sklon té přímky m je roven –Ea lomeno R. A tak pokud dostanete sklon této přímky, můžete vypočítat aktivační energii. Pokud byste chtěli dostat frekvenční faktor, průsečík s osou y je roven přirozenému logaritmu A, což je frekvenční faktor. Můžete ho tedy vypočítat, pokud chcete. Pokud dáte přirozený logaritmus rychlostní konstanty na osu y, tady nahoru, a potom 1 lomeno teplota na osu x, tohle bude naše osa x. Spočítal jsem to dopředu, abych ušetřil trochu času. Pokud vezmete přirozený logaritmus této rychlostní konstanty tady, dostanete tuto hodnotu. A pokud vezmete 1 lomeno touto teplotou, dostanete tuto hodnotu. Takže teď máme nějaké datové body. Máme x a y a máme tato data z různých bodů, která můžeme dát do kalkulačky a vypočítat sklon této přímky. Udělejme to, zadejme tyto hodnoty. Jdeme na Stat a potom na Edit a dvakrát zmáčkneme Enter a potom začneme zadávat. Takže x, to bude 0,00213. Takže když je x rovno 0,00213, y je rovno –9,757. Zadejme další bod. Když se x rovná 0,00208, y se bude rovnat –8,903. Náš třetí bod je když x je rovno 0,00204 a y se rovná –8,079. Dále máme 0,002 a máme –7,292. A nakonec poslední bod bude 0,00196 a potom –6,536. Takže jsme všechno zadali do kalkulačky. Opusťme tohle, vraťme se do Stat a půjdeme na Calc. A dvakrát zmáčkneme Enter. Chceme lineární regresi, takže zmáčkneme tohle a dostaneme naši lineární regresi. Vidíme tady, že b je sklon. Takže to je –19149 a průsečík s osou y bude 30,989 tady. Zapišme si to. Takže teď víme z kalkulačky, že y se rovná m bylo –19149x a b bylo 30,989. Snažíme se vypočítat aktivační energii, takže nás zajímá sklon přímky. Sklon je –19149. A těchto pět bodů jsem si zakresli do grafu tady dole. Vidíte, že tu mám přirozený logaritmus rychlostní konstanty na ose y a 1 lomeno teplota na ose x. A tady mám těch pět bodů, které jsem právě zadal do kalkulačky. Takže sklon naší přímky je roven –19 149, to jsme teď spočítali. Abychom našli aktivační energii, víme, že sklon m je roven… Změním barvu, abych to zdůraznil. Sklon je roven –Ea lomeno R. Takže sklon je –19 149 a to je rovno minus aktivační energie lomeno plynová konstanta. A R, jak jsme viděli v minulých videích, je 8,134. Odsud si vyjádříme aktivační energii. Vytáhneme si naši kalkulačku. Tohle zrušíme. Bude to 19 149 krát 8,314. A dostaneme tedy aktivační energii rovnu 159 205, přibližně J na mol. Náš výsledek má být v kJ na mol, to je tedy přibližně 159 kJ/mol. Zapišme si to. Aktivační energie se rovná 159 kJ/mol. Využili jsme tedy všechna data, která jsme dostali a spočítali jsme aktivační energii v kJ/mol. V části b) máme opět najít aktivační energii opět v kJ/mol. Ale tentokrát můžeme použít pouze rychlostní konstanty při dvou různých teplotách, při 470 a 510 Kelvinů. Takže musíme použít tu druhou formu Arrheniovy rovnice, o které jsme mluvili v předchozím videu. Byl to přirozený logaritmus druhé rychlostní konstanty k2 lomeno první rychlostní konstantou k1 se rovná –Ea lomeno R, Ea je opět aktivační energie, krát 1 lomeno T2 minus 1 lomeno T1. A pro naše teploty 510, to bude T2 a potom 470 bude T1. Zadejme tedy, co už víme. Přirozený logaritmus... Musíme si vyhledat tyto rychlostní konstanty, to uděláme za chvíli. Čemu se rovnají k1 a k2? A to se bude rovnat minus aktivační energie, kterou se snažíme spočítat, lomeno plynová konstanta, což víme je 8,314. To bude krát 1 lomeno T2, kdy T2 je 510. 1 lomeno 510 minus 1 lomeno T1, což je 470. Takže 1 lomeno 470. Teď se podívejme na hodnoty těch rychlostních konstant. Hledáme tedy rychlostní konstanty při dvou různých teplotách. A naše teploty jsou 510 K. Změním si barvy. Hledáme tedy k1 a k2 při 470 a 510 K. Vraťme se zpět nahoru do tabulky. Takže 470, to bylo T1. A to bude hodnota první rychlostní konstanty, 5,79 krát 10 na –5. A potom T2 byla 510, to bude naše druhá rychlostní konstanta. 1,45 krát 10 na –3. Zadejme tyto hodnoty zpět do naší rovnice. Bude to k2 lomeno k1, tedy 1,45 krát 10 na –3 lomeno 5,79 krát 10 na –5. Zadejme to tedy. Bude to přirozený logaritmus 1,45 krát 10 na –3 lomeno 5,79 krát 10 na –5. Teď z toho tedy musíme spočítat aktivační energii. Vypočítejme nejprve to nalevo. Přirozený logaritmus 1,45 krát 10 na –3, a to vydělíme 5,79 krát 10 na –5. a dostaneme zaokrouhlíme to na 3,221. Dostaneme tedy 3,221 na levé straně. Na pravé straně máme –Ea lomeno 8,314. Vyřešme teď tohle. Vytáhneme si zase kalkulačku. Napišme 1 děleno 510. Od toho odečteme 1 děleno 470. Uvidíme, co dostaneme. Dostaneme, zaokrouhlím to na –1,67 krát 10 na –4. Máme tedy –1,67 krát 10 na –4. Teď už to jen vyřešíme pro aktivační energii. Máme tedy 3,221 krát 8,314 a potom to musíme vydělit 1,67 krát 10 na –4. A dostaneme aktivační energii rovnu přibližně 160 kJ/mol. Náš výsledek má být v kJ/mol a ne J/mol, takže přibližně 160 kJ/mol. Aktivační energie se tedy rovná přibližně 160 kJ/mol, což je téměř stejná hodnota, kterou jsme dostali využitím toho druhého tvaru Arrheniovy rovnice. S tím druhým tvarem jsme dostali 159 kJ/mol, to je hodně blízko. Můžete tedy využít oba tvary Arrheniovy rovnice, podle toho, jaké je zadání příkladu.

0:00
11:06