Reakční kinetika (10/19) · 7:14
Integrovaný tvar rychlostní rovnice pro reakce 2. řádu Z diferenciální rovnice si odvodíme, jak závisí koncentrace látky v závislosti na čase pro reakce 2. řádu.
Řekněme, že máme reakci druhého řádu pro látku A. Takže látka A se přeměňuje v produkty. Na začátku reakce začínáme s počáteční koncentrací A. Po nějakém čase t budeme mít koncentraci A v čase t. Pokud chceme vyjádřit rychlost reakce, naskytuje se několik možných způsobů. Můžeme říct, že rychlost se rovná záporné změně koncentrace látky A za určitý čas. Dělali jsme to v předchozích videích. Můžeme taky říci, že se rychlost rovná, podle rychlostní rovnice, rychlostní konstantě k krát koncentrace látky A. A pokud se jedná o druhý řád pro A, mluvíme o reakci druhého řádu, jedná se o koncentraci A na druhou. Tyto dvě rovnice se sobě rovnají. Můžeme říct, že tato část se rovná této. Máme tedy zápornou změnu koncentrace A za čas, což se rovná rychlostní konstantě k krát koncentrace A na druhou. Teď se musíme zamyslet nad výpočtem. Na místo vyjádření tohoto jako průměrné rychlosti změny A za čas, budeme přemýšlet nad okamžitou rychlostí. Tedy rychlost změny koncentrace A podle času. Máme záporné d[A], tedy d koncentrace A, lomeno dt, tedy rychlost změny koncentrace A podle času t. A to se rovná k krát A na druhou. A máme naši diferenciální rovnici. Můžeme tuto rovnici vyřešit a získat funkci. První věc, co uděláme k vyřešení naší rovnice, je separace proměnných. Potřebujeme dostat A na jednu stranu a t na druhou stranu, tedy dt na druhou stranu. Vydělíme obě strany A na druhou, takže nalevo teď máme minus d[A] lomeno koncentrace A na druhou, a vynásobíme obě strany dt. Dostaneme tak k krát dt na pravé straně. Teď jsme připraveni integrovat. Takže budeme integrovat a přepíšeme si, co máme na levé straně. Takže tohle bude minus. Napíšu to jako koncentrace A na minus druhou d[A], aby se s integrálem trochu lépe pracovalo. A na pravé straně máme stále k dt. Tak jsme připraveni integrovat. Budeme integrovat levou stranu tady a pravou stranu tady. K je konstanta, takže ji neintegrujeme. Vraťme se zpátky sem a vzpomeňme si, odkud budeme integrovat. Na čas se podívejte tady. Začínáme v čase 0 a pokračujeme do času t. A co se týče koncentrace, vycházíme z počáteční koncentrace do koncentrace v čase t. Teď tedy vložíme tato data do rovnice. To znamená, že integrujeme od 0 po t, tedy 0 až t. A integrujeme od počáteční koncentrace po koncentraci v nějakém čase t. Tak co máme na levé straně? Co je náš integrál? Je to jako x na minus druhou dx. Takže je to integrál x na minus druhou dx. To nám dá koncentraci A na minus prvou lomeno –1. Zřejmě jste už někdy počítali s integrály, jestli sledujete toto video. A pak tady máme znaménko minus. Takže já to tady připíšu. Toto záporné znaménko tady pořád zůstává. A když to vyhodnotíme, toto se bude rovnat... Takže to je to stejné jako 1 lomeno koncentrace A. Máte tedy dvě minus, z čehož vzniká plus. Takže toto bude 1 lomeno koncentrace A, protože A na minus prvou je 1 lomeno koncentrace A. Počítáme to od výchozí koncentrace po koncentraci v čase t. Na pravé straně máme integrál dt, což je pouze t. Máme tedy kt od 0 po t. Dále využijeme základní větu integrálního počtu. Takže půjdeme dál a dosadíme, co máme. Nejdříve dosadíme tohle. Takže mám 1 lomeno koncentrace [A]t minus 1 lomeno počáteční koncentrace A, a na pravé straně to bude samozřejmě jen kt. Tak jsme tedy našli integrovanou rychlostní rovnici pro reakci druhého řádu. Tohle je naše integrovaná rychlostní rovnice. Můžeme to nazvat integrovaný rychlostní zákon. Je celkem jedno, který název použijete. Ale tato rovnice je velmi užitečná, protože ji můžeme upravovat. Můžeme přesunout 1 lomeno počáteční koncentrace A na pravou stranu a dostaneme 1 lomeno koncentrace A se rovná kt plus 1 lomeno počáteční koncentrace A. A to vypadá velmi povědomě. Toto je rovnice přímky. Vidíme, že to je y se rovná mx plus b. Když znázorníte čas na osu x a na osu y zakreslíte 1 lomeno koncentrace A, dostanete přímku. A sklon této přímky, tedy m, by měl odpovídat k, rychlostní konstantě. A průsečík osy y, což je b, bude 1 lomeno počáteční koncentrace A. Pojďme si tady v rychlosti nakreslit graf. Máme naše osy. Na osu x dosadíme čas. Takže na osu x dosadíme čas a na osu y dosadíme 1 lomeno koncentrace A. Takže máme 1 lomeno koncentrace A. A pokud se jedná o reakci druhého řádu, graf by měl tvořit přímku. Takže já tady nakreslím přímku, nebo se o to alespoň pokusím. A sklon této přímky se rovná k. Rovná se rychlostní konstantě. To jsme viděli tady, sklon se rovná rychlostní konstantě. A průsečík s osou y, což je tento bod, by mělo být 1 lomeno počáteční koncentrace A. Tento bod je tedy 1 lomeno počáteční koncentrace A. Tohle je tedy integrovaný tvar rychlostní rovnice pro reakci druhého řádu.
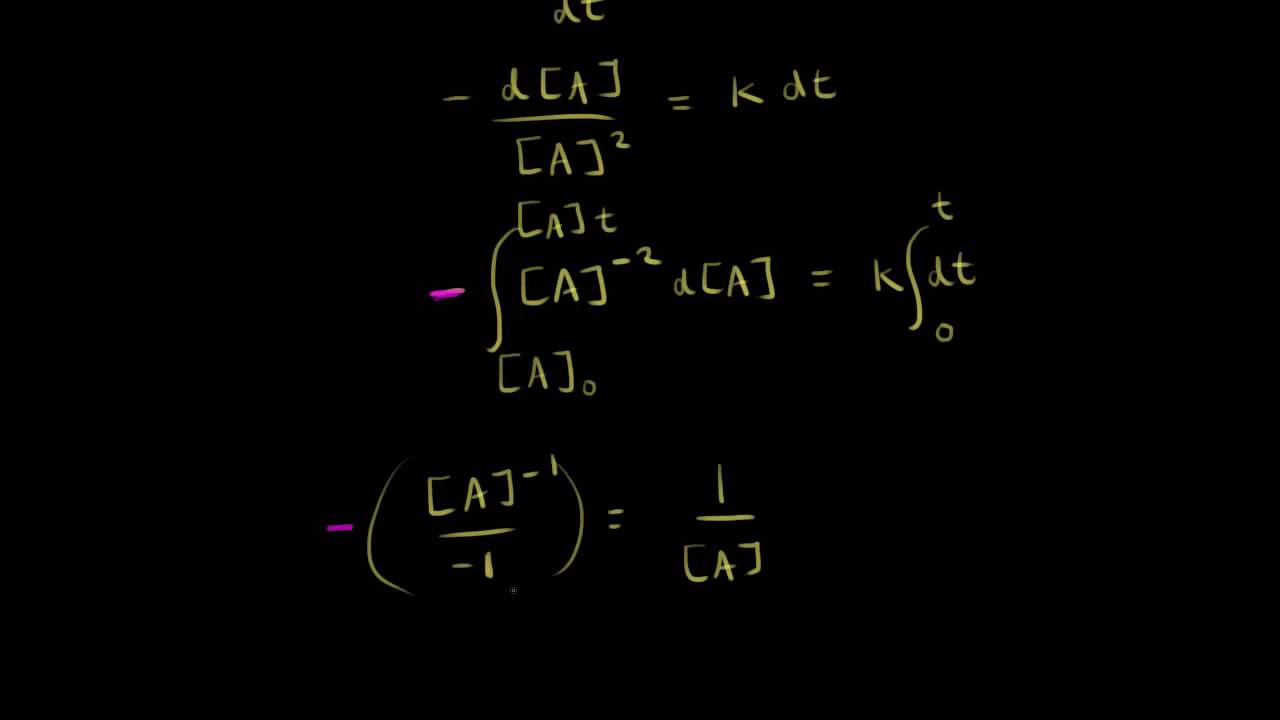
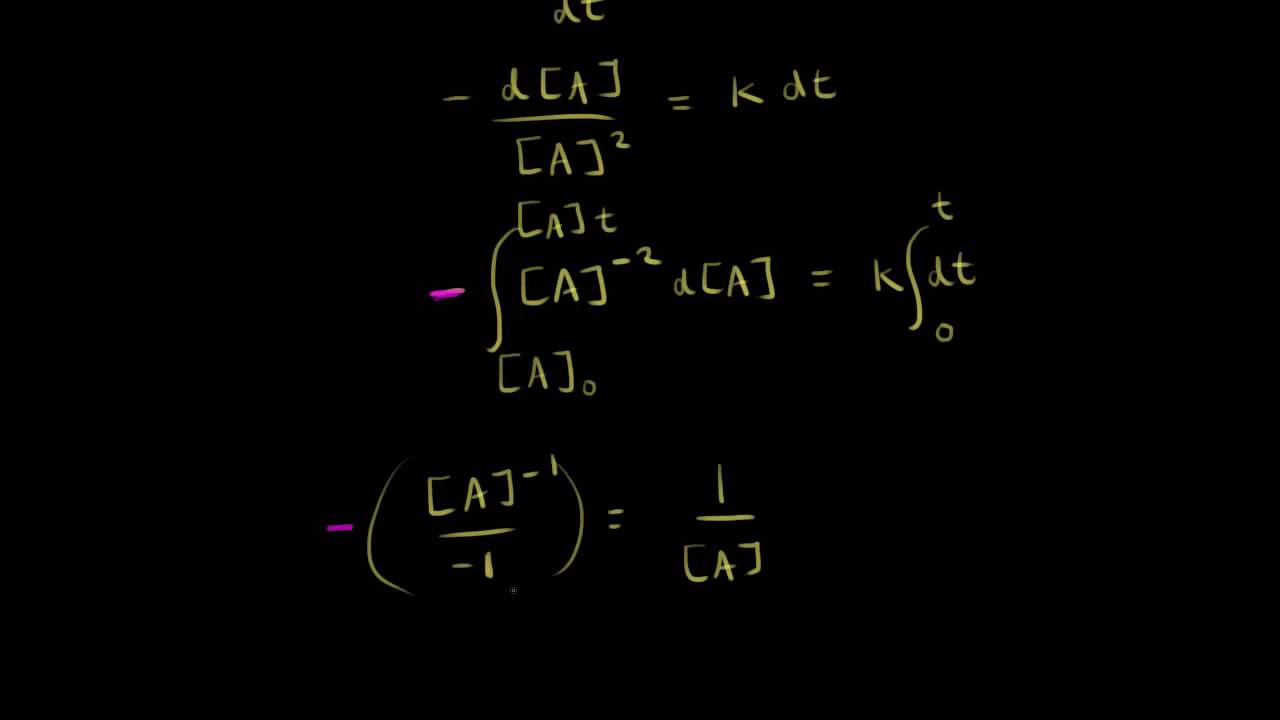
0:00
7:14