Grafy funkcí s absolutní hodnotou Zde si pěkně krok po kroku ukážeme, jak z funkčního předpisu funkce můžeme vyčíst informace, pomocí kterých můžeme nakreslit graf.

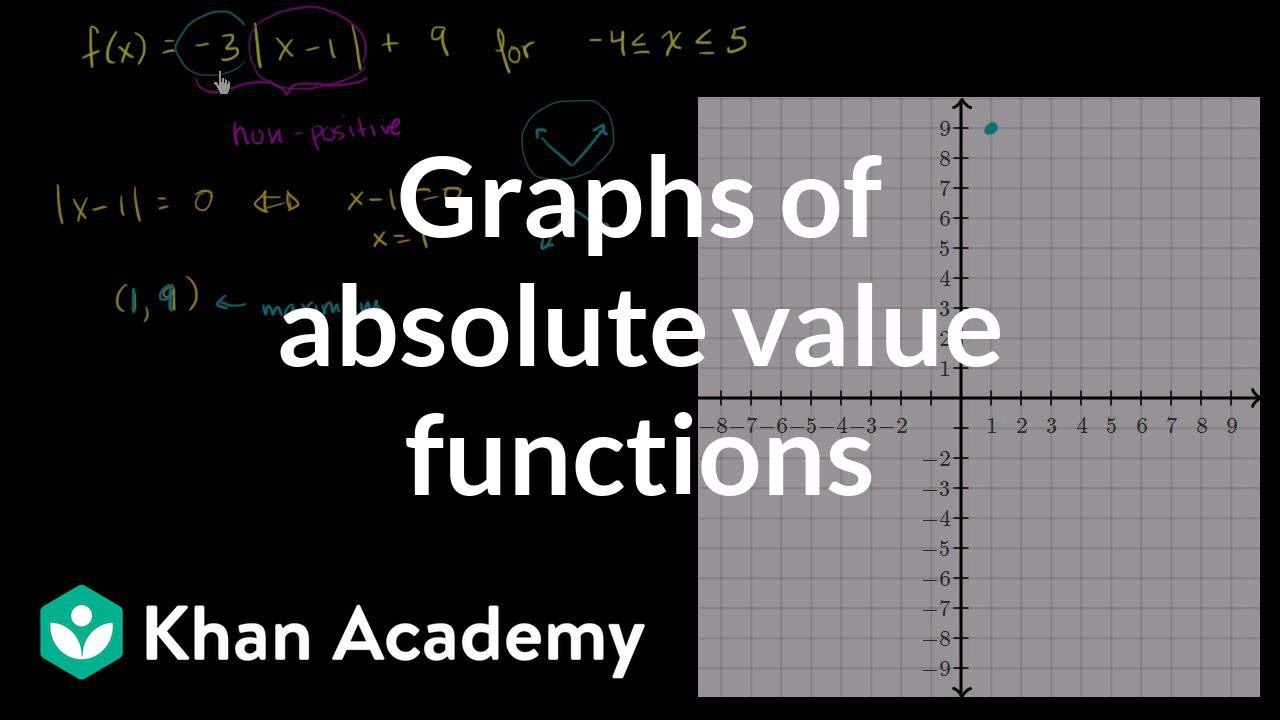
Pojďme maličko prozkoumat grafy funkcí s absolutní hodnotou. Jednu tu mám, její předpis je roven minus 3 krát absolutní hodnota z (x minus 1) plus 9. Máme omezený definiční obor na interval od minus 4 do 5 včetně. Doporučuji vám si zastavit video a zkusit si načrtnout graf. Můžete to udělat tak, že budete dosazovat do předpisu čísla z definičního oboru a vždy jen dopočítáte příslušnou funkční hodnotu. Pojďme se ale zamyslet nad průběhem této funkce. Kde tato funkce dosáhne maxima a kde minima? A kde bude mít vrchol? Pojďme se na to podívat bez dosazování bodů. Máme tu tedy absolutní hodnotu. Tato absolutní hodnota, stejně jako jakákoli jiná, je vždy nezáporná. My tuto kladnou absolutní hodnotu násobíme záporným číslem. Tento první člen vznikne vynásobením záporného a nezáporného čísla, proto víme s naprostou určitostí, že bude nekladný. Proč říkám nekladný? Protože může být záporný, ale také roven nule. Tento první člen bude tedy buď 0 nebo záporné číslo. Tohle je tedy vždy nekladné. Jakou nejvyšší hodnotu zde můžeme dosáhnout? Nejvyšší hodnota je dosažena, pokud je absolutní hodnota rovna 1. Když je absolutní hodnota, potom celý člen je roven 0 a funkce má své maximum. Konkrétně s funkční hodnotou 9. Za jakých podmínek se tato absolutní hodnota rovná 0? Zamysleme se nad tím. Kdy se absolutní hodnota z (x minus 1) rovná 0? Bude se rovnat 0, pokud x minus 1 se bude rovnat 0. K oběma stranám rovnice přičtu 1 a získám x se rovná 1. V bodě x je rovno 1 je naše funkce v maximu. Absolutní hodnota je nulová, a proto celý první člen je nulový. Zjistili jsme, že maximum je v bodě (1,9) Vyznačme si ho na grafu. Změním jeho barvu, aby byl lépe vidět na bílém pozadí. Maximum naší funkce má souřadnice (1,9). Je dobré si též uvědomit, že je to zároveň vrchol grafu s absolutní hodnotou. Bod (1,9) se nachází právě zde. Můžeme už odhadnout, jak bude graf vypadat. Obecný graf funkce s absolutní hodnotou vypadá nějak takto...nebo takto. První případ odpovídá tomu, pokud je koeficient před ní kladný. V tomto případě se rozevírá směrem nahoru. Ale protože je náš koeficient záporný, budeme to mít otevřené směrem dolů. Ve vrcholu má tato funkce své maximum. O tom jsme již mluvili před chvílí. Jak to bude ale vypadat dál? Jak se funkce bude chovat napravo od vrcholu a jak nalevo? Ve skutečnosti to nemusíme dělat obecně. Můžeme jen dosadit krajní body definičního oboru. Rád bych to však pořádně prozkoumal. Pojďme si tuto funkci rozdělit na dvě části. Potom funkční hodnota z x je rovna... ...rozdělíme to teď na dvě části. První část bude popisovat pravou stranu od vrcholu. A ta druhá část bude popisovat levou stranu od vrcholu. Pravou stranu bude popisovat nerovnice: 1 je menší nebo rovno x, a to je menší nebo rovno 5. A tu levou bude popisovat... ...tohle byla část napravo. Pro levou část budeme mít předpis... ...napíšu to jinou barvou. Bude to minus 4 je menší nebo rovno x, a to je menší než 1. Připomínám, že definiční obor zkoumané funkce je interval od minus 4 do 5. Tento interval vyznačím na číselné ose. A teď ho rozdělíme na pravou a levou stranu. Od jedničky doprava to patří k pravému ramenu funkce. A naopak od jedničky doleva to přísluší levému ramenu funkce. Tedy pro tu pravou stranu, kde je x mezi 1 a 5, je tato absolutní hodnota... ...nebo jinak, pokud je x větší než 1, x minus 1 je kladné a absolutní hodnota z kladného čísla je stále to samé kladné číslo. Tedy pro x je větší nebo rovno než 1 bude mít naše funkce předpis: minus 3 krát (x minus 1) plus 9. Ještě můžeme závorku roznásobit, minus 3 krát (x minus 1). Já to tu napíšu, abychom viděli ten jednodušší výraz. Bude to tedy... ...trochu si to tu posunu. Pro x je větší než 1 nemusíme vůbec řešit tu absolutní hodnotu. Bude to tedy minus 3 krát (x minus 1) plus 9. To je minus 3 krát x plus 3 plus 9, což je minus 3 krát x plus 12. Tady napíšu minus 3 krát x plus 12, což platí pro x je větší nebo rovno 1. Povšimněme si zde zajímavé věci. Směrnice grafu je zde záporná, konkrétně je rovna minus 3. Začínáme od tohoto bodu a vedeme úsečku se směrnicí minus 3. To v praxi znamená, že pokaždé, když se ve směru osy x posuneme o jedno políčko, na ose y se propadneme o tři políčka dolů. A znovu a znovu. Takto tedy vypadá směrnice s hodnotou minus 3. Teď tyto naznačené body pospojuji, aby to bylo hezky vidět. Nakreslím to fialově. Bude to vypadat právě takto. Ještě ten předpis fialově zarámuji, aby to bylo jasné. Tato část naší funkce bude vypadat tak, jak jsem právě nakreslil. Co ten druhý případ, když je x menší než 1? Když je x menší než 1, x minus 1 je záporné. To znamená, že absolutní hodnota bude měnit znaménko výrazu uvnitř. Pokud je tedy x menší než 1, potom se absolutní hodnota z (x minus 1) bude rovnat minus (x minus 1). To můžu ještě přepsat jako 1 minus x. Naše funkce se potom bude rovnat minus 3 krát (1 minus x) plus 9. Což je to samé jako... ...roznásobím závorku... Je to to samé jako minus 3 plus 3x plus 9. Což se rovná 3x plus 6. Zde je důležité si uvědomit, že tento graf má kladnou směrnici, s hodnotou 3. Také rovnou vidíme, že máme průsečík s osou y v šestce. Tady ten bod vyznačím a přímka bude vypadat takto. Směrnice je plus 3, což znamená, že když se x zvýší o 1, y se zvýší o 3. Zvýším x o 1, tím se zvýší y o 3. Nebo naopak, pokud x snížím o 1, y se potom sníží o 3. A znova a znova. Spojím body a bude to vypadat takto. A máme hotovo. Vytvořili jsme graf této rovnice s absolutní hodnotou. Toto video jsem vytvořil za účelem hlubšího poznání tohoto tématu. Existuje však i rychlejší verze řešení. Mohli jste si prostě říct, že tato funkce bude nabývat svého maxima v bodě 1. Tento první člen totiž je v jedničce nulový. Tím jsme zjistili, že vrchol bude v bodě (1,0). A potom stačí jen dosadit krajní body definičního oboru. S tím, že víme, že krajní body jsou s vrcholem spojeny úsečkou. Tedy vypočítám funkční hodnotu v bodě minus 4 a 5. Tím získám body, ve kterých funkce končí a pak už je jen spojím s vrcholem. Teď tomu však už rozumíme více, což je vždy užitečné.