Rovnice s neznámou pod odmocninou (6/9) · 5:23
Řešení rovnic s odmocninou - ověření pravosti kořenů Na dalším příklad na rovnici s odmocninou si znovu ukážeme důležitost provádění zkoušky. Pro jeden kořen zkouška vyjde a pro druhý ne.
Navazuje na
Lineární rovnice o dvou neznámých.
Takže, řekněme, že máme rovnici s odmocninou 2x minus 1 se rovná druhá odmocnina z (8 minus x). Takže už máme odmocninu osamostatněnou na jedné straně rovnice. Můžeme si říct: "Stačí se jen zbavit odmocniny." "Umocníme obě strany rovnice na druhou." Takže se dá říct, že je to stejné jako: (2x minus 1) na druhou se rovná (druhá odmocnina z (8 minus x)) na druhou. Dostaneme: (2x minus 1) na druhou je 4x na druhou minus 4x plus 1 se rovná 8 minus x. Teď ale musíme být velmi, velmi opatrní. Můžeme si říct: "Fajn, rovnici jsme upravili dobře, udělali jsme to samé na obou stranách." "Tohle jsou ekvivalentní rovnice." Ale ve skutečnosti nejsou úplně ekvivalentní. Když totiž něco umocňujete na druhou, můžete se na to dívat tak, že přicházíte o informace o původní rovnici. Takže například tohle by bylo správné řešení i kdyby původní rovnice byla 2x... (Udělám to jinou barvou.) I kdyby původní rovnice byla: 2x minus 1 se rovná minus druhá odmocnina z (8 minus x). Protože kdybyste umocnili obě strany téhle rovnice, tak byste také dostali tohle stejné řešení, protože druhá mocnina je stejná z kladného i záporného čísla. Takže když hledáme řešení k této rovnici, musíme napřed ověřit, že je to správné řešení pro naši původní žlutou rovnici, a ne pro tuhle rovnici nahoře. Pokud je to řešení pro tuto rovnici napravo, a ne pro tuto žlutou, pak se jedná o nepravý kořen rovnice. Takže to zkusíme vyřešit. Napíšeme to v základním kvadratickém tvaru. Z obou stran odečteme 8. Tím se zbavíme osmičky odtud a k oběma stranám přičteme 'x'. Takže, plus x, plus x, a tady dostaneme... 4x na druhou minus 3x minus 7 se rovná 0. A podívejme, tohle chceme rozložit na součin, a možná by to šlo, kdybych... Hm, použiju kvadratický zápis, tady. Takže řešení budou... 'x' se bude rovnat -b, takže 3 plus nebo minus odmocnina z (b na druhou), (-3) na druhou je 9, minus 4 krát 'a', což je 4, krát 'c', což je -7. Takže bych mohl říct krát... No, prostě sem napíšu 7 a tohle minus mi z tohohle udělá plus. To celé děleno 2a. Takže 2 krát 4 je 8. Takže tohle bude 3 plus nebo minus druhá odmocnina z... 4 krát 4 je 16, to celé krát 7. 16 krát 7 je 70, plus 42. Ujistím se, že to dělám správně. Takže 16 krát 7. Dva, čtyři. Takže to je 112 plus 9. Takže 121, to sedí dobře. Takže plus nebo minus druhá odmocnina ze 121, to celé děleno 8. To se rovná 3 plus nebo minus 11, to celé děleno 8. Když přičteme 11, dostaneme 14/8. Nebo když odečteme 11, 3 minus 11 se rovná -8. -8 děleno 8 se rovná -1. Takže se musíme zamyslet... Můžete si říct: "Fajn, našel jsem dvě řešení." Ale nezapomeňte, jedno z nich může být řešením pro tuto odlišnou rovnici, která zmizela, když jsme obě strany umocnili. Musíme zjistit, zda jsou to skutečné kořeny rovnice, nebo je jeden z nich nepravý. Ve skutečnosti je jedno z nich velmi pravděpodobně řešením této rovnice, kterou jsme původně nechtěli řešit. Takže se podívejme... Vyzkoušíme 'x' se rovná -1. Pokud se 'x' rovná -1, dostaneme 2 krát (-1) minus 1 rovná se druhá odmocnina z (8 minus (-1)) , což je -2 minus 1 se rovná druhá odmocnina z 9. Takže máme -3 se rovná druhá odmocnina z 9. Kladná druhá odmocnina z 9. Tohle je kladná druhá odmocnina. Tohle není správně. Takže tohle je nepravý kořen rovnice. Nepravý. Nepravý kořen rovnice. Je to řešení k téhle rovnici. Protože, všimněte si, pro tuhle rovnici, když nahradíte 2 krát (-1) minus 1 se rovná minus odmocnina z (8 minus (-1)). Takže tohle je -3 se rovná -3. Takže tohle platí. Tohle je tedy nepravý kořen. A tohle tedy bude správné řešení pro naši původní rovnici, což si můžete ověřit sami. Vlastně bych vás k tomu chtěl vyzvat.
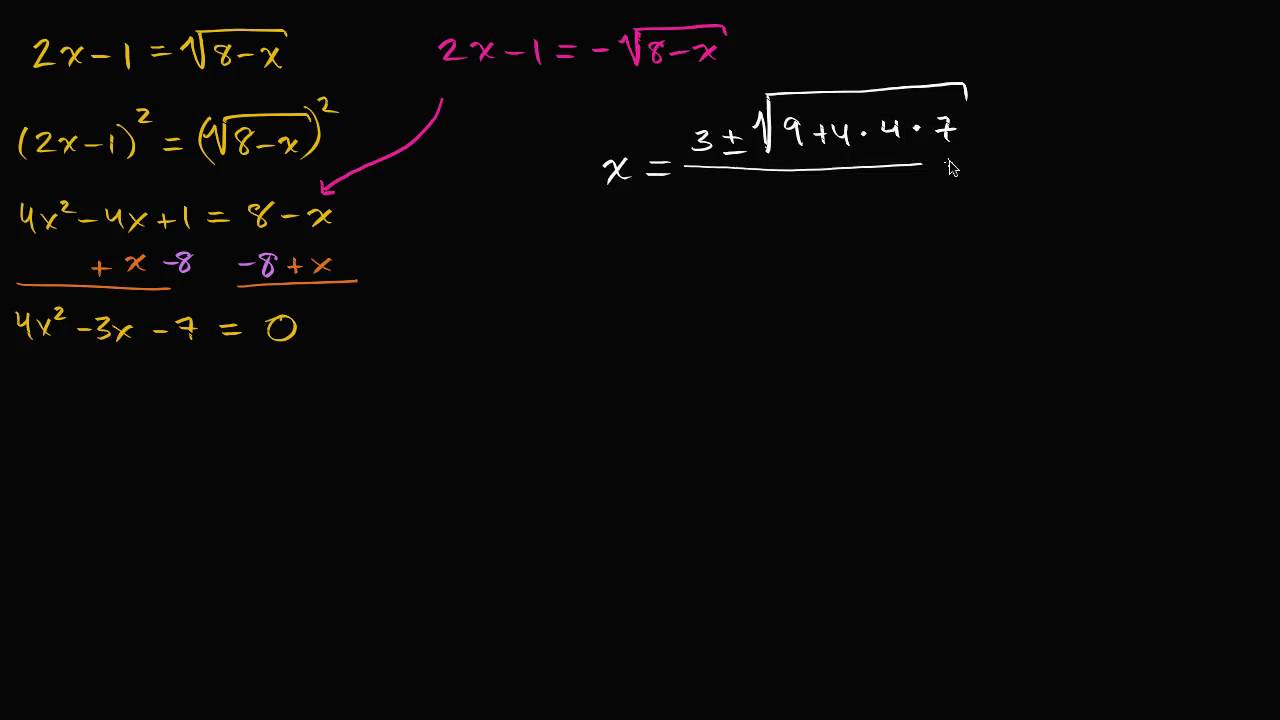
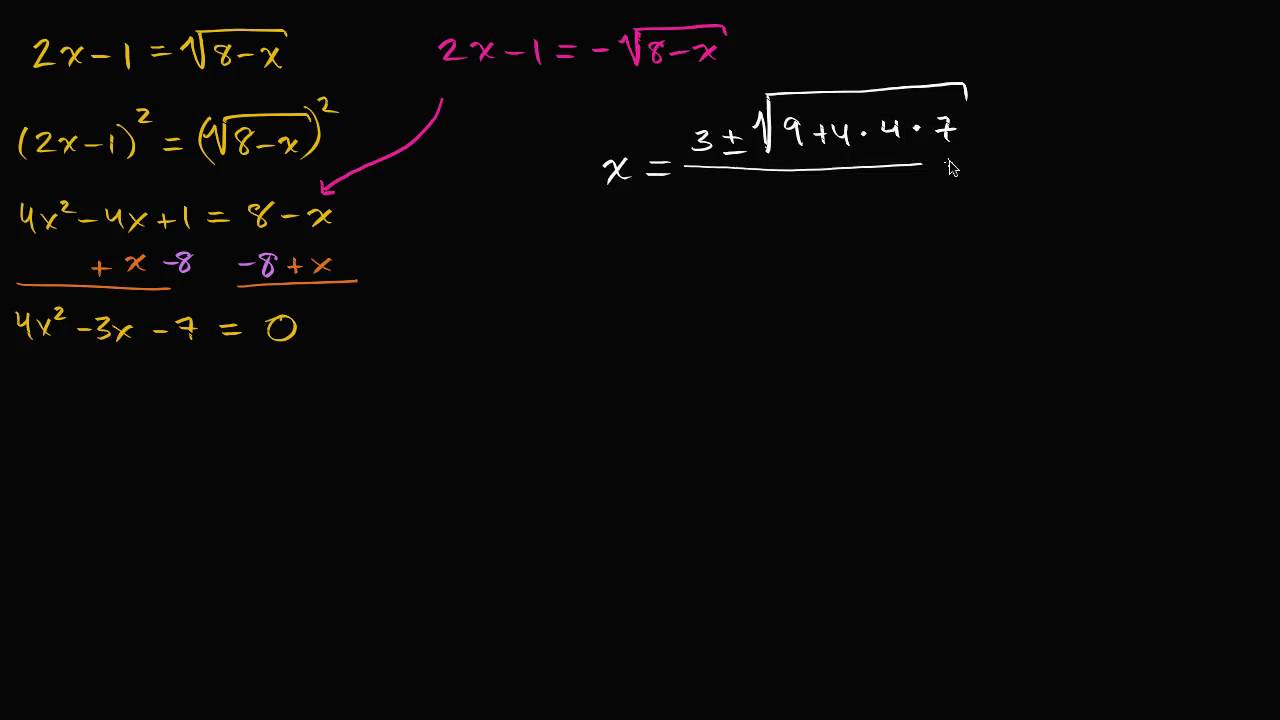
0:00
5:23