Určení grafu podle kořenů Naším úkolem je podle kořenů (tedy průsečíků s osou x) zjistit, který ze tří grafů odpovídá zadanému mnohočlenu.

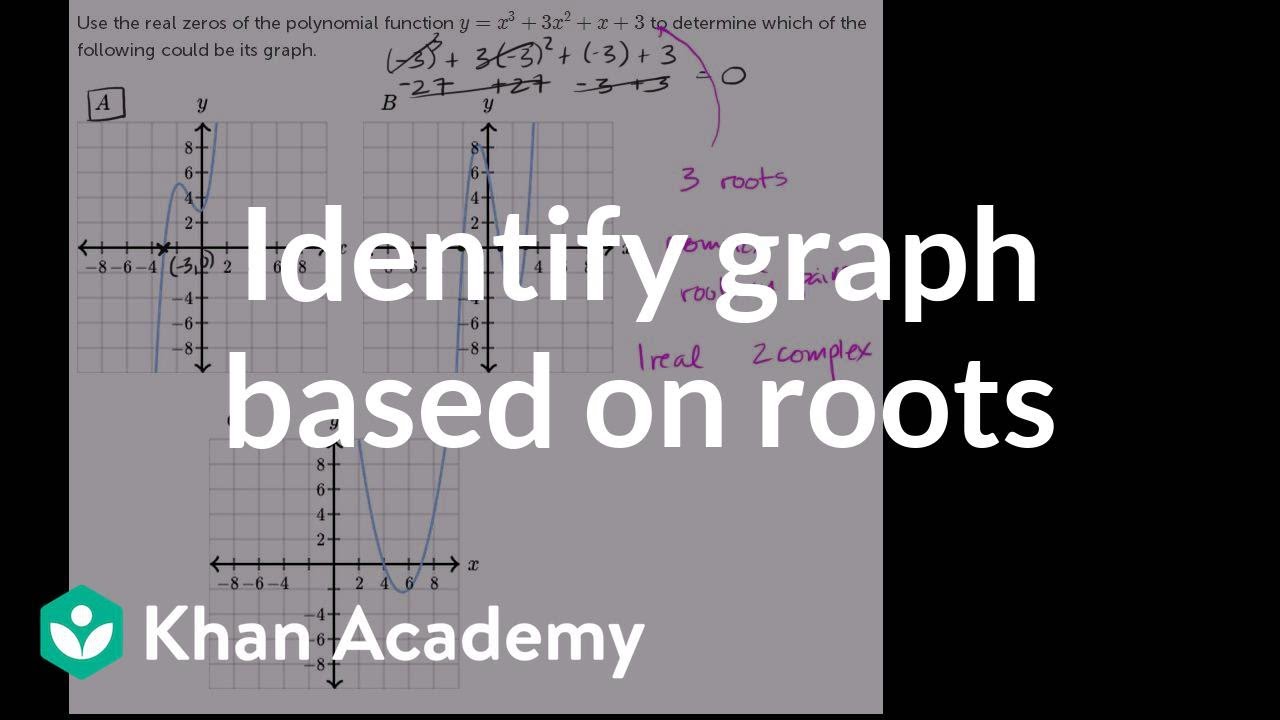
Použijte reálné kořeny mnohočlenu předepsaného rovnicí 'y' je rovno 'x na třetí' plus 3 krát 'x na druhou' plus 'x' plus 3 a určete, který graf rovnici odpovídá. Je hned několik způsobů, jak k tomuto přistupovat. Mohli bychom určit nebo odhadnout kořeny těchto grafů a zjistit, zda je funkce skutečně rovna 0, když se 'x' rovná oněm bodům. Například v grafu A… Nejprve bych vám, jako obvykle, doporučil pozastavit video a zkuste to vyřešit sami, než ukážu, jak na to. Předpokládám, že jste to zkusili. Podívejme se na první graf. Jeho kořen… Funkce je rovna nule přímo v tomto bodě. Když se podíváme na graf, zdá se, že 'x' je rovno -3. Když to odhadnu. Vypadá to tedy, že je to bod [-3, 0]. Podívejme se, zda dosazením -3 za 'x' dostaneme, že 'y' je rovno 0. Takže '-3 na třetí' plus 3 krát '-3 na druhou' plus -3 plus 3. Co nám to dá za výsledek? Toto je -27, toto je +27, toto je samozřejmě -3, toto je +3. Tyto se odečtou. Tyto se odečtou. Skutečně se to rovná nule. Toto bylo celkem jednoznačné, obrázek A je grafem zadané rovnice. Můžeme zkusit graf B, ale musíme ověřit, že funkce nabývá nuly v bodě -2, dále v bodě, zdá se, 1 a nakonec v bodě 3. Jelikož už víme, že A je správná odpověď, žádná z hodnot 'x' je -2, 1, nebo 3 by neměla způsobit, že je funkce rovna 0. Uvidíte, že to nefunguje. Tento taky. Když za 'x' dosadíte 4 nebo 7, nedostanete 0 , protože ve správném grafu se funkce nerovná nule pro 'x' rovno 4 nebo 7. Další nápovědou, že to nebude ta funkce, je, že tam jsou celkem 3 kořeny. Jenom to napíšu. Budou celkem 3 kořeny. Kořeny mohou být buď reálné nebo komplexní. Velkou nápovědou je, že komplexní kořeny jsou ve dvojicích. Komplexní kořeny jsou ve dvojicích. Takže může být situace se třemi reálnými kořeny, toto má 3 reálné kořeny, i když víme, že toto není ten správný graf funkce, nebo když existuje jeden komplexní kořen, musí tam být k němu i druhý. Jestliže tam tedy jsou komplexní kořeny, pak další možností je jeden reálný a dva komplexní kořeny. Toto má dva reálné kořeny, to není přípustné. Naznačovalo by to, že tam je jediný komplexní kořen, což není možné. Další způsob, jak k tomu přistupovat, což by byl delší způsob, ale dejme tomu, že zde ty grafy nejsou a jen byste museli najít kořeny, pak byste to mohli rozložit na součin. Toto lze snadno rozložit. 'y' je rovno 'x na třetí' plus 3 krát 'x na druhou' plus 'x' plus 3. Jak víme z dřívějších videí, rozkládat mnohočleny vyššího než druhého stupně je tak trochu umění. Ale často, když je to potřeba, členy můžete seskupit zajímavými způsoby, obzvlášť když vidíte, že několik členů má společné činitele. Například tyto dva členy mají společného činitele 'x na druhou'. Když to vytknete, dostanete 'x na druhou' krát (x plus 3), což je pěkné, protože se to podobá těmto dalším dvěma členům. Mohli bychom to napsat jako 1 krát (x plus 3). A pak vytkneme (x plus 3). Vytkneme (x plus 3) a dostaneme (x plus 3) krát ('x na druhou' plus 1). A teď najdeme nulové body. Toto celé je rovno 'y'. Pamatujte, toto celé se rovná 'y'. 'y' se rovná nule, jestliže se jakýkoliv z těchto činitelů rovná 0. Kdy se (x plus 3) rovná 0? Odečteme od obou stran 3. 'x' se rovná -3. Kdy se 'x na druhou' rovná 0? Pardon, kdy se ('x na druhou' plus 1) rovná 0? Když se 'x na druhou' rovná -1. Pro toto nejsou žádná reálná 'x', neexistuje reálné číslo 'x', pro které je 'x na druhou' rovno -1. 'x' bude imaginární, nebo obecněji, bude to komplexní číslo. Ještě jednou, budeme mít dvojici komplexních kořenů a jeden reálný kořen 'x' je rovno -3.