Úvod do normálního rozdělení Základní koncept normálního rozdělení a distribučních funkcí.

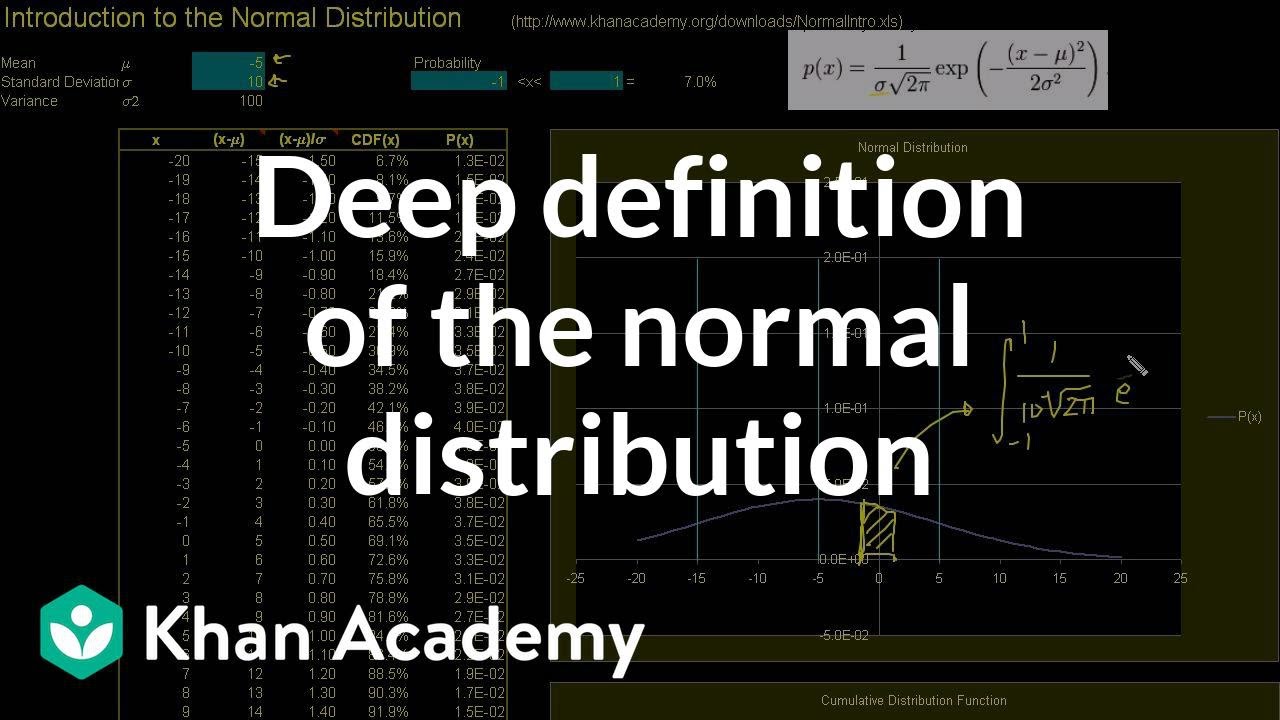
Normální rozdělení je jedním z nejdůležitějších klíčových konceptů statistiky. Vše, nebo alespoň téměř vše, čeho se v inferenční statistice snažíme docílit, tedy vyvodit závěry na základě nasbíraných dat, je do určité míry založeno na normálním rozdělení. Co bych tedy rád v tomto videu a na příkladech dokázal, je, abyste odcházeli s co největším porozuměním normálního rozdělení. Aby kdykoli Vám někdo v budoucnosti řekne, že předpokládal normální rozdělení, jste si mohli říct, "Ano, to znám," Takhle vypadá předpis funkce, chápu, co značí, jak jej použít, apod. Tahle tabulka s daty je ke stažení na www.khanacademy.org/downlads/ a pokud se na danou stránku podíváte uvidíte tam všechno, co je možné si stáhnout. Stáhlněte si download/normalintro.xls a dostanete přesně tuhle tabulku, kterou tu mám já. Mám dojem, že jsem to uložil ve správném formátu. Každopádně, když půjdete na Wikipedii a zadáte normální rozdělení nebo když si ho vyhledáte -- vlastně si můžu zapnout elektronické pero -- najdete něco takového. Doslova jsem tu tabulku nakopíroval z Wikipedie. Chápu, že to může vypadat strašidelně, když tu máte všechna ta řecká písmena, ale je to -- tahle sigma tady -- to je jen směrodatná odchylka rozdělení. Budeme si s touhle tabulkou chvíli hrát a ukážeme si, co to všechno znamená. Nejspíš víte, co to směrodatná odchylka znamená, ale toto zde je směrodatná odchylka rozdělení, což je funkce hustoty pravděpodobnosti. A já vám doporučuji se znovu podívat na video o funkcích hustot pravděpodobnosti, neboť pochopení binomického rozdělení, které je diskrétní (nespojité), plynule navazuje na tuto látku. Binomické rozdělení Vám říká, jaká je pravděpodobnost, že Vám vyjde 5, a Vy se jen tak kouknete na histogram nebo sloupový graf a řeknete si, tady jí máme. Ale ve spojitém rozdělení pravděpodobnosti nebo ve spojité funkci hustoty pravděpodobnosti nemůžete jen tak z grafu vyčíst pravděpodobnost, že Vám vyjde 5. Musíte se ptát, jaká je pravděpodobnost, že dostanu něco mezi 4,5 a 5,5. Musíte funkci dát nějaký rozsah. A ani poté není tato pravděpodobnost jen tak čitelná z grafu. Pravděpodobnost je daná obsahem plochy pod funkcí. Bude dána tímto obsahem. Pro ty z Vás, kdo umíte derivovat a integrovat, pokud je funkce p(x) naše funkce hustoty rozdělení -- nemusí to být normální rozdělení i když povětšinou je -- pak způsob, jak spočítáte pravděpodobnost výskytu jevu řekněme mezi 4,5 a 5,5. Řekněme, jaká já pravděpodobnost že zítra naprší něco mezi 4,5 a 5,5 palci vody? Tato pravděpodobnost bude ve skutečnosti integrál pro rozsah 4,5 a 5,5 této funkce hustoty rozdělení nebo této funkce hustoty rozdělení, funkce p(x). Takže to je jen obsah pod křivkou. Těm z Vás, kdo ještě integrovat neumí, doporučuji shlédnout videa patřičného kurzu. (pozn. překl. Calculus) Ale v jednoduchosti Vám toto popisuje obsah pod křivkou odsud až posud. Ukazuje se, že u normálního rozdělen to není úplně snadné spočítat analyticky, a tak to spočítáte numericky. Nemusíte se cítit provinile, že nevíte, jak tuto funkci zintegrovat. Existují pro to vlastní funkce a dokonce to celé můžete aproximovat Jedním ze způsobů, jak si věc ulehčit je aproximovat ji stejně jako jiné integrály. Můžete se ptát, jaký je tenhle obsah? A je to přibližně obsah tohoto lichoběžníku. Takže můžete spočítat obsah lichoběžníku, s použitím průměru těhle dvou bodů a znásobením dělkou jeho základny. Nebo jen použijete výšku -- jen si změním barvy protože mám pocit, že je tam moc zelené -- nebo můžete vzít výšku této úsečky zde a zde a znásobit je délkou jejich podstavy. Dostanete obsah tohoto obdélníku, který můžete považovat za docela dobrý odhad pro obsah plochy pod křivkou. Jasné? Protože Vám tady trochu přebývá, ale zároveň Vám tady trochu chybí, můžete to považovat za docela dobrý odhad. To je vlastně to, co ukazuji v druhém videu, jen odhad plochy pod křivkou pro lepší představu přeměny binomického rozdělení na normální rozdělení při velkém množství měření. Co je zajímavé pro normální rozdělení -- nejsem si jistý zda jsem to už nezmiňoval -- je toto tady, ... tohle je ten graf. Jen tak na okraj, někteří zde mohou zmínit centrální limitní teorém. A tohle je skutečně asi nejdůležitější nebo nejzajímavější věc ve vesmíru, centrální limitní teorém. Nebudu ho zde dokazovat, ale co nám říká, a možná byste mu již mohli rozumět, Vy, kdo jste viděli mé druhé video, kde se bavíme o házení mincí. Kdybychom házeli mincí -- což lze považovat za nezávislé jevy -- a kdyby jste sečetli všechny z Vašich hodů, a kdybyste si měli dát bod -- za každou hlavu, co hodíte -- a kdybyste je sečetli, tak s tím, jak se blížíte nekonečnému množství hodů, blížíte se i normálnímu rozdělení. Co je zajímavé je, že v každém z pokusů -- v případě házení mincí je pokus jeden hod mincí -- každý z pokusů se nemusí řídit normálním rozdělením. Takže bychom se mohli bavit o molekulárních interakcích a pokaždé, když sloučenina x rekaguje se sloučeninou y, pak výsledek jejich reakce nemusí mít normální rozdělení. Ale když sečtete tisíce těchto interakcí, pak zničeho nic výsledek bude podléhat normálnímu rozdělení. Toto je důvod, proč se jedná o tak zásadní rozdělení. Neustále se objevuje v přírodě, a pokud nasbíráte data z něčeho, co je velice komplexní a co je suma pravděpodobně mnoha téměř nekonečna nezávislých pokusů, je poměrně dobrým předpokladem, že výsledek bude mít normální rozdělení. Budou tu další videa, kde si povíme něco o tom, kdy je to dobrý odhad a kdy nikoli. Ale každopádně, nechme to teď trochu uležet a já tohle nejspíš přepíšu. Tohle je to, co uvidíte na Wikipedii, ale co může být napsáno jako 1 nad sigma krát odmocnina ze 2 pí krát exp znamená tohle celé na e. Takže dostaneme e na tento výraz, což je -x mínus průměr to celé na druhou děleno 2 sigma na druhou. Toto je směrodatná odchylka. Směrodatná odchylka na druhou je rozptyl. Takže abyste chápali, jak toto použít, tak -- páni tady je docela dost řeckých písmen, co s tím dělat? -- Toto mi ukazuje na výšku funkce normálního rozdělení. Řekněme, že toto je rozdělení osob s výškou nad 1,80 m. (5 stop 9 palců) Řekněme, že tohle bylo 1,80 a ne 0. Co mi to tedy říká je, že pokud byste chtěli zjistit, jaká je pravděpodobnost, že narazíte na někoho, kdo má přibližně o 12 centimetrů (5 palců) víc, než je průměr, co byste potřebovali udělat je že byste potřebovali tohle číslo, těch 12 cm převést na x. A pak byste znali směrodatnou odchylku, protože jste už měřili víckrát a máte víc vzorků. A víte, že rozptyl je směrodatná odchylka na druhou. Dále znáte průměr, a pak jen vložíte x semhle a ono Vám to už poví, jaká je výška celé funkce. A pak funkci musíte dát rozsah. Protože nemůžete jen chtít vědět, kolik lidí má přesně o 12 cm víc než je průměr. Potřebujete ve skutečnosti říct, kolik lidí má mezi 11 a 13 cm víc, než je populační průměr. Musíte tomu dát trochu rozsahu, protože nikdo není přesně na atom vyšší o dokonalých 12 cm víc, než je průměr. Samotná definice centimetru není vymezená natolik přesně. To je jak byste tuto funkci využili. Tento princip se často vyskytuje zaprvé v přírodě, ale zejména v inferenční statistice, a měli byste se s co nejlépe a nejpodrobněji seznámit. Takže se na to podívejte. Teď si chvíli budeme s touto rovnicí hrát, jen abychom si ujasnili, jak vše funguje apod. Kdybych si měl vzít jen toto -- rád bych Vám pomohl si to pořádně zapamatovat -- můžu to přepsat, vzít sigma sem do odmocniny a pak vzít směrodatnou odchylku semhle, a stane se z ní 1 děleno odmocninou ze 2 pí sigma na druhou. Nikdy jsem to v této podobě neviděl napsané, ale dává mi to náhled na to, že sigma na druhou pokaždé zapisujeme jako sigma na druhou, ale je to jen rozptyl a rozptyl je co spočítáte před tím, než spočítáte směrodatnou odchylku, což je zajímavé. A pak, tahle část, tu můžete přepsat jako e na -1/2 krát a obě z nich jsou na druhou, takže můžeme klidně napsat x mínus průměr děleno sigma na druhou. A toto poměrně dobře vyjasňuje, co se tu děje. Protože co je tohle? x mínus sigma je vzdálenost mezi jakýmkoli bodem který chceme nalézt. Řekněme, že jsme tady.. x mínus mí je průměr, takže to je zde a toto je vzdálenost, a toto je směrodatná odchylka, která je ve skutečnosti vzdálenost. Takže toto zde mi říká, kolik směrodatných odchylek jsem vzdálený od průměru. Což ve skutečnosti nazýváme standardní z-skór, mluvil jsem o tom v druhém videu. A pak, když umocníme toto na druhou a vezmeme toto na mínus 1/2- No, raději to přepíšu. Když bych měl napsat e na -1/2 a, to je to samé jako e na a to celé na -1/2, že? Když něco umocníte a pak umocníte výsledek, můžete jen znásobit mocnitele. Takže podobně, toto můžete přepsat jako 1 děleno odmocnina z 2 pí sigma na druhou což je rozptyl. A teď si jen hraji s rovnicí, protože Vám chci ukázat možné varianty, abyste získali celkový náhled a pochopení. Pokud Vás napadne, proč tomu tak je a získáte to toho hlubší vhled, napište mi email. Ještě jednou, mám za to, že je úžasné, že najednou tu máme tuto rovnici, ve které je pi a e. Tolik jevů je tímto popsatelných a pí a e se objevují pohromadě tak často, jak často je e na i pí rovno -1. Něco Vám to říká o celém vesmíru. Každopádně, můžu toto přepsat jako e na x mínus mí děleno sigma na druhou a to celé na -1/2. Něco, co je na -1/2, je jen 1 děleno odmocninou, což je to samé co už máme tady. Takže můžeme tohle celé přepsat jako 1 děleno odmocninou ze dvou pí krát rozptyl krát e, abychom dostali z-skór na druhou. Pokud řekneme, že z-skór je toto, z-skór je počet směrodatných odchylek od průměru, z-skór na druhou. A tak se to najednou vyčistí. Můžeme vzít 2 pí krát rozptyl krát e na počet směrodatných odchylek od průměru a následně to umocnit. A pak vezmeme odmocninu výsledku a převrátíme ji a získáme normální rozdělení. Každopádně, chtěl jsem tohle ukázat. Mám za to, že je to zajímavý způsob, jak si s tím pohrát. Pak, když to uvidíte v kterékoli jiné podobě, nezděsíte se, co to je, "Já myslel, že normální rozdělení vypadá takhle nebo takhle." Když to je tedy venku, pojďme si ještě trochu pohrát s touto funkcí normálního rozdělení. Takže tady máte vykresleno normální rozdělení. Můžete změnit vstupní hodnoty, které jsou v tomto případě vyvedeny zelenou a modrou. Takže právě teď to vykresluje graf s průměrem nula a směrodatnou odchylkou 4. Sem jenom napíšu rozptyl, jen aby to bylo jasné, rozptyl je směrodatná odchylka na druhou. A co se stane, když změníme průměr? Takže když průměr změníme z 0 na řekněme 5. Všimněte si, že se nám graf jen posunul o 5. Jasné? Měl střed zde, nyní má střed tady. Pokud to změníme na -5, co se stane? Celá křivka se posune od středu o 5 doleva. Teď co se stane, když změníte směrodatnou odchylku? Rozptyl je průměrná vzdálenost od středu, směrodatná odchylka je odmocnina téhož. Takže je to ve skutečnosti, ne úplně, ale tak trochu průměrná vzdálenost od průměru. Takže čím menší směrodatná odchylka, tím blíže se body budou přibližovat k průměru. Měli bychom tak získat tak trochu úžší graf tak se podívejme, zda se to povede. Když je směrodatná odchylka dva, vidíme rozdíl. V tomto grafu je mnohem pravděpodobnější, že budete blízko průměru než dále od něj. Pokud zvolíte směrodatnou odchylku větší, řekněme 10, najednou dostanete graf, který je dost plochý a tahle část se zdá ubíhat donekonečna. A to je zásadní rozdíl: binomické rozdělení je vždy konečné. U binomického rozdělení musíte mít konečný počet hodnot, zatímco u normálního rozdělení je pravděpodobnost definována pro všechna reálná čísla. Takže pravděpodobnost, pokud máte průměr -5 a směrodatnou odchylku 10, pravděpodobnost že dostanete 1000 je velmi malá, ale existuje. Existuje i pravděpodobnost, že se všechny atomy mého těla najednou uspořádají tak dokonale, že propadnu židlí, na které sedím. Je to velice nepravděpodobné, a pravděpodobně se to nestane za dobu existence vesmíru, ale ta pravděpodobnost tu je. A ta může být popsána skrze normální rozdělení, protože to říká, že cokoli se může stát, přestože je to nadmíru nepravděpodobné. To, o čem jsem tu mluvil na začátku videa je, že když máte graf normálního rozložení pro Vaši situaci, nemůžete jen ta kouknout na bod -- jen si zas vezmu elektronické pero -- ale musíte vyřešit obsah plochy mezi dvěma body. Takže, co jsem chtěl říci -- řekněme, že toto je normální rozdělení -- a já se zeptám, jaká je pravděpodobnost, že dostaneme 0. Nemám tušení, jaké jevy tento graf popisuje takže mluvme o jevu v bodě 0. Pokud se zeptám konkrétně na 0, pak je pravděpodobnost 0 -- neměl bych používat stále 0 -- protože obsah plochy pod křivkou, přesně pod bodem 0, je 0, neboť je to jen úsečka. Proto se musíte ptát na rozsah. Takže Vás bude zajímat řekněme pravděpodobnost mezi -- a vlastně to sem mohu napsat -- mezi mínus 0,005 a plus 0,005 -- přibližně -- říká nám to, že jsou blízko 0. Udělám to raději mezi -1 a 1. Vyšlo nám 7 procent a hned si ukážeme jak jsem se k tomuto dostal. Takže si vezmu kreslítko- Takže co jsme to právě udělali? Mezi 1 a -1 -- a já vám ukáže trochu zákulisí toho, co nám Excel provádí -- dostaneme se z -1, což je přibližně tady, k 1. A počítáme obsah oblasti pod křivkou. Potřebujeme spočítat tady tuto plochu, pro ty z Vás, kdo znají integrace, počítáme integrál mezi -1 a 1 této funkce, kde směrodatná odchylka je tady, takže vidíme 10, a průměr je -5. Raději to napíšu. Takže počítáme, pro tyto vstupní hodnoty, jak je to znázorněno zde, normální distribuční funkce, směrodatná odchylka je 10 krát odmocnina ze 2 pí krát e na -1/2 krát x mínus náš průměr. Náš průměr je teď záporný. Náš průměr je -5, takže to máme x plus 5 děleno směrodatnou odchylkou na druhou, což je rozptyl, takže to dává 100 na druhou dx. Což dělá to, co už máme tady, těchto 7 procent nebo přesněji 0,07, což je obsah plochy zde. Bohužel pro nás, toto není lehký integrál pro analytický výpočet, ani pro nás, kdo integrovat umí. Takže to většinou děláme numericky. A poměrně jednoduchý způsob -- no, ne zas tak jednoduchý -- je skrze funkci, která se nazývá kumulativní distribuční funkce a která je ideální pro výpočet této plochy. Takže co to kumulativní distribuční funkce ve skutečnosti je -- budu ji nazývat kumulativní distribuční funkce -- je to funkce proměnné x. A dává nám obsah pod křivkou, touto křivkou. Takže řekněme, že toto je x, naše x. Říká nám, jaký je obsah pod funkcí až k bodu x. Tedy jinak řečeno, dává nám informaci o pravděpodobnsoti, že se objeví nějaká hodnota menší než hodnota x. Takže se jedná o obsah plochy od mínus nekonečna až k x naší funkce hustoty pravděpodobnosti. Když použijete Excelovskou normální distribuční funkci, řekněme norm rozdělení. Musíte mu zadat hodnotu x, zadáte mu průměr, zadáte směrodatnou odchylku. A potom mu řeknete, zda chcete kumulativní distribuci, v tom případě zadáte true, nebo normální distribuci, v tom případě false. Takže když byste chtěli graf, jako je tento zde, musíte zadat false velkými písmeny (FALSE). Pokud byste chtěli graf kumulativní distribuční funkce, který mám tady dole -- jen si to posunu trochu níž, zbavím se elektronického pera, aby kumulativní distribuční funkce byla -- přesně tady, tak Excelu řeknete při zadání příkazu TRUE. Takže toto je kumulativní distribuční funkce pro ty samé hodnoty Toto je normální rozdělení, toto je kumulativní rozdělení. Jen abyste měli představu. Pokud Vás zajímá, jaká je pravděpodobnost, že dostanu hodnotu menší než 20? Neboli jakoukoli hodnotu pod 20 v tomto rozdělení. Kumulativní rozdělení zde -- jen ho trochu upravím aby bylo vidět -- pokud se podíváte na dvacet, tak jen najdete patřičný bod a vidíte, že pravděpodobnsot 20 a méně je poměrně vysoká. Je téměř 100 procent. Což dává smysl, neboť většina plochy pod touto křivkou je méně než 20. Nebo pokud by Vás zajímalo, jaká je pravděpodobnsot -5 a méně? Tak -5 je průměr, takže polovina vašich výsledků by měla být pod a polovina nad. A pokud se podíváte na tento bod, ihned uvidíte, že zde máme 50 procent. Takže pravděpodobnost méně než -5 je přesně 50 procent. Takže co uděláte, když Vás zajímá pravděpodobnost jevu mezi -1 a 1 je -- jen si zase vezmu svoje elektronické pero -- najdete si, jaká je pravděpodobnost, že se vyskytne -1 a méně. Takže tato celá oblast. A potom zjistíte pravděpodobnost 1 a méně, což je celá oblast zde -- dám ji asi trochu jinou barvu -- 1 a méně je všude zde. A když odečteme žlutou oblast od purpurové, tak dostaneme všechno, co nám zbude zde. Což je přesně to, co jsem udělal v tabulce. Jen sjedu dolů. Tohle je asi na můj počítač trochu moc, když to nahrávám. Takže co jsem udělal bylo, že jsem zhodnotil kumulativní distribuční funkci v bodě 1 zde. A kumulativní distribuční funkci v bodě -1, což je zde. A rozdíl mezi nimi, odečtu toto od tohoto a to mi v podstatě řekne pravděpodobnost výskytu jevu mezí těmito dvěma body. Nebo jinými slovy, obsah této plochy. Velice Vám doporučuji, abyste si s tím v Excelu pohráli a prošmejdili příkazy a vůbec všechno. Tato oblast zde bude -1 a +1. Takže když znáte graf, tak tahle přímka ve středu zde, značí průměr. A pak tyto dvě, které jsem nakreslil zde, to jsou 1 směrodatná odchylka pod a jedna směrodatná odchylka nad průměrem. Někteří lidé se můžou ptát, jaká je pravděpodobnost výskytu jevu vzdáleného jednu směrodatnou odchylku od průměru? To se dá snadno spočítat. Co můžu udělat, je kliknout sem. A to mi dá pravděpodobnost výskytu jevu jednu směrodatnou odchylku -- průměr je -5 -- jednu odchylku pod průměrem (-15) a jednu směrodatná odchylka nad průměrem, což je 10 plus -5, tedy 5. Takže hledáme mezi 5 a 15. Což nám dá 68,3 procent. 68,3 procenta vychází vždy, když Vás zajímá pravděpodobnost, že se jev vyskytne méně než jednu směrodatnou odchylku od průměru, v případě, že má normální rozdělení. Takže opět, toto číslo znázorňuje obsah plochy pod křivkou zde. A způsob, jakým se k němu dostanete, je s pomocí kumulativní distribuční funkce. Sjedu trochu níž. Pokaždé, když s tím chci sjet se musím zbavit pera. Když se podíváte na hodnotu v bodě 5, která je zde. Tak ta je jednu směrodatnou odchylku nad průměrem, což je číslo přibližně tady. Vypadá jako přibližně 80 procent, možná 90 procent. A pak se podíváte na hodnotu v jedné směrodatné odchylce pod průměrem, což je mínus 15. A ta vypadá zhruba jako 15 procent, 15,16, možná řeknu 18 procent. Ale výsledek dostanete, když odečtete ttuto hodnotu od této hodnoty, nebo´t to se dostanete k oblasti mezi nimi. A to proto, že tato hodnota udává pravděpodobnost, že jste níže. Takže když se podíváte na kumulativní distribuční funkci, dostanete toto. Pořád mi to jezdí sem a tam A když se podíváte na 5 -- což je tady -- tak to Vám v podstatě říká, že tato oblast pod křivkou, pravděpodobnost výskytu jevu 5 a méně, tak to je všechno zde. A když získáte i výsledek pro mínus 15 zde, dostanete pravděpodobnost jevu, který je tady. Proto když odečtete tuto hodnotu od této vyšší, zbude vám pouze plocha pod touto částí křivky. Jen abyste této tabulce porozuměli lépe, protože bych opravdu rád, kdybyste si s tím pohráli a viděli, co se stane, když změním průměr z mínus 5 na plus 5. Celé se to posunulo doprava. Pouze se to posunulo doprava o pět. Jejda. Jen si vezmu pero. Posunulo se to doprava o 5. Pokud bych chtěl zmenšit směrodatnou odchylku, pak bychom viděli, jak se celé rozložení jakoby smrskne. zkusíme 6. A najednou to vypadá mnohem špičatěji, a když to upravíme na 2, stane se ještě užší. Opravdu bych rád, kdybyste si s tím pohráli a opravdu se snažili tomuto konceptu porozumět, zejména kumulativní distribuční funkci, a zamysleli se, jak souvisí s binomickým rozložením, které jsem rozebíral v posledním videu. Abych to vynesl do grafu, jen jsem vzal každý z těchto bodů. A zakreslil jsem body mezi -20 a +20 a to pouze v inkrementech jedné. To bylo moje rozhodnutí, postupovat po jedné. Takže se nejedná o spojitou křivku, ale jen o zanášení bodů a jejich spojování úsečkami. Poté jsem spočítal vzdálenost každého z těchto bodů od průměru. Takže tady jsem vzal 0 mínus 5, takže tady je jejich vzdálenost. Toto vám říká, že v bodě mínus 20 máme hodnotu o 25 menší než je průměr. To je všechno. Pak jsem tuto hodnotu vydělil směrodatnou odchylkou a dostal jsem z-skór, standardní z-skór. Toto mi říká, kolik směrodatných odchylek je mínus 20 vzdáleno od průměru. V tomhle případě 12,5 směrodatných odchylek od průměru. Pak jsem tuto hodnotu vzal a dosadil jsem ji do téhle rovnice, abych zjistil jaká je výška funkce v tomto bodě. Řekněme v mínus 20 je výška velice nízká. V mínus 2 je to trochu lepší, výška bude přibližně, nejspíš asi někde tady. A tak získám tuto hodnotu. Ale abych zjistil pravděpodobnost tohoto jevu, musím ještě spočítat kumulativní distribuční funkci. Takže toto je pravděpodobnost, že jste níže než toto. Takže tato oblast je dost malá. Není to nula, ale vypadá to jako nula, ale jen protože jsem zaokrouhlil. Bude to asi 0,0001, takže to vyjde jako hodně malé číslo. Existuje i pravděpodobnost, že nám vyjde mínus 1000. Další z věcí, které byste opravdu měli chápat. je proč musí integrál celé této oblasti křivky vycházet 1, protože ten musí počítat se všemi možnými jevy. A to by se mělo stát, pokud vložíme opravdu malé číslo sem a opravdu velké číslo sem. Tak, tady to máte, máme 100 procent. Přestože toto není úplně 100 procent. Museli bychom to spočítat pro mínus nedkonečno až k plus nekonečnu abychom se dostali na pravých 100 procent. Tady to je pouze zaokrouhlení. Je to pravděpodobně něco jako 99,99999 procent. A tak, abychom to spočítali, vezmeme si hodnotu kumulativní distribuční funkce v tomto bodě a odečteme od ní hodnotu kumulativní distribuční funkce v tomto bodě. A tak se nám objeví těch 100 procent. každopádně, doufám, že jste se v normálním rozdělení trochu zorientovali. Opravdu bych rád, kdybyste si s tou tabulkou pohráli a pokusili se si případně vytvořit vlastní. V budoucnu dokonce tento typ tabulky budeme používat jako vstupní bránu k jiným modelům. Pokud budeme kupříkladu zpracovávat finanční model a řekneme si, že příjem má normální rozdělení okolo zadané očekávané hodnoty, jaké je normální rozdělení našeho celkového příjmu. Nebo se budeme zabývat jedním ze stovek různých příkladů ,jako je tento. Každopádně, budu se na Vás těšit v dalším videu.