Vzdálenost mezi bodem a přímkou Pokud máme vypočítat vzdálenost bodu od přímky, můžeme to udělat pomocí kolmice, která bude procházet bodem. Poté už počítáme jen vzdálenost dvou bodů.

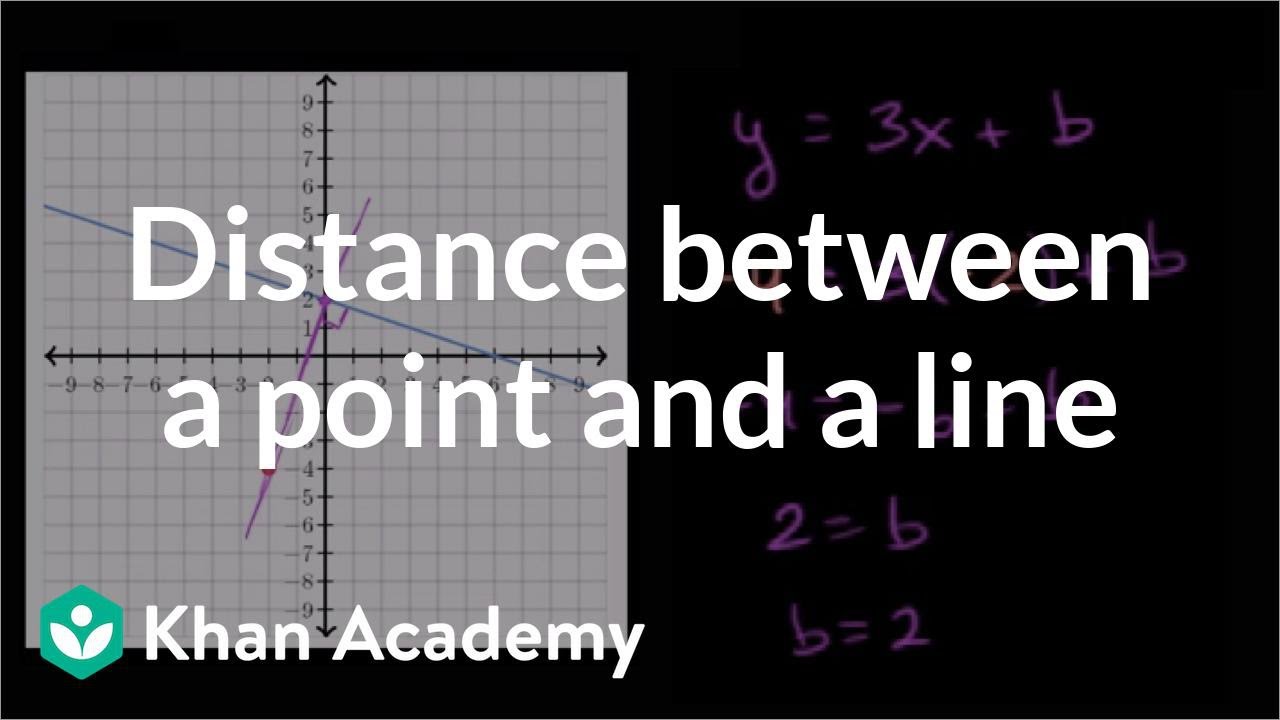
Najděte vzdálenost mezi bodem –2, –4, přesně tento bod, a mezi přímkou y rovná se –1/3x plus 2, což je tato přímka. Na to potřebujeme najít kolmici k této modré přímce, y rovná se –1/3x plus 2, která prochází tímto bodem. Takže potřebujeme zjistit rovnici této přímky. A potom musíme určit, kde se tyto dvě přímky protínají a pak musíme najít vzdálenost mezi oběma průsečíky, čímž dostaneme nejkratší vzdálenost mezi tímto bodem a touto přímkou. Takže první krok spočívá v určení sklonu této kolmice. Sklon této kolmice bude záporně převrácený ke slonu této modré přímky. Takže záporně převrácená hodnota k –1/3 bude +3. Takže tady tato přímka bude mít sklon 3. Takže ji lze zapsat ve tvaru y rovná se 3x plus b, kde "b" je průsečík přímky a osy y. Vypadá to, takto od oka, že se to bude blížit hodnotě 2. Ale pojďme si to ověřit. Abychom zjistili, co teda b vlastně je, pojďme si nahradit tady tento bod. Víme, že tato přímka má sklon 3, a že tento bod na ní musí ležet. Takže tenhle bod musí splňovat tuto rovnici. Když x je –2, y je –4. Takže dostáváme –4 se rovná 3 krát –2 plus b. Dosadím tam –2. 3 krát –2 plus b. A teď můžeme zjistit "b". Máme –4 se rovná –6 plus b. Přičteme 6 na obě strany rovnice, takže dostaneme 2 se rovná b, nebo taky b se rovná 2. Měli jsme tak pravdu. Průsečík na ose y pro druhou přímku je v hodnotě 2. Takže od pohledu vídíme, si můžeme ověřit, kde se obě protínají. Protínají se na ose y v bodě y se rovná 2. Pro obě platí, že když se x rovná 0, y se rovná 2. Pokud to nebylo jasné, můžeme tyto dvě rovnice vzájemně porovnat. Mohli bychom si říct, máme 3x plus 2. My už víme, že to opravdu je 3x plus 2, protože b je 2. A kdy se tedy 3x plus 2 rovná –1/3x plus 2? No, to uvidíme. Když od obou stran odečteme 2, kdy se pak 3x rovná –1/3 x? Nabízí se vlastně několik možností, které bychom mohli zkusit. Mohli bychom přičíst 1/3x k oběma stranám rovnice. To bychom dostali 3 a 1/3, což je to stejné, jako 10/3x se rovná 0. A pokud bychom obě strany vynásobili 3/10, vyšlo by nám, že x se rovná 0. Přímky se pak protínají, pokud se x rovná nule. Pro obě přímky platí, že když se x rovná 0, y je 2. x se rovná 0, y se rovná 2. Ale to bylo zřejmé už od pohledu. Mohli jste si všimnout, že oba průsečíky na ose y se rovnají 2, právě když x je rovno 0. Takže tady tento bod má souřadnice [0,2]. My už víme, že tady tento bod je bod –2, –4. A teď nám jen zbývá najít vzdálenost mezi oběma body. Vzorec pro vypočet vzdálenosti je vlastně použití Pythagorovy věty. Musíme najít vzdálenost jako změnu na ose y a jako změnu na ose x. To provedeme postupně. Takže na ose y, jaká je tato vzdálenost? My jsme vlastně přešli od y se rovná –4, k y se rovná 2. Tady ta vzdálenost mezi těmito body je 6. A jaká je tato vzdálenost tady? Tady bylo x nejprve rovno –2, a potom se x rovnalo 0. Tady ta vzdálenost je 2. Takže vzdálenost mezi oběma body je v podstatě jen přepona pravoúhlého trojúhelníku se stranami 6 a 2. Pokud si toto označíme jako vzdálenost d, můžeme říct, že vzdálenost na druhou se rovná… Vlastně jsem jen přeformuloval vzorec pro vzdálenost. Ten vzorec jen sděluje, že y2 minus y1, což je šest, na druhou. To je v podstatě Pythagorova věta. Je to stejné, jako tvrdit, že 6 na druhou plus x2 minus x1, což je 0 minus –2, což je 2, na druhou se bude rovnat vzdálenosti na druhou. A my vidíme, že to je opravdu jen Pythagorova věta. Pojďme si tak teda vypočítat vzdálenost. Vzdálenost na druhou se tak bude rovnat 36 plus 4, což je 40. A vidíme tedy… 40… vzdálenost na druhou…nebo můžu napsat… Vzdálenost je rovna druhé odmocnině 40. Druhou odmocnina 40 lze napsat jako druhou odmocninu ze 4 krát 10. Takže je to stejné. Potom se teda vzdálenost rovná 2, odmocníme-li částečně 4. Je to druhá odmocnina 4 krát druhá odmocnina 10. 2 je druhá odmocnina 4. Takže 2 krát druhá odmocnina 10. A máme hotovo.