Pravděpodobnostní rozdělení (4/7) · 11:05
Binomické rozdělení 2 Více o binomickém rozdělení.
Navazuje na
Kombinatoriku.
V minulém videu jsme definovali náhodnou proměnou X, jako počet hlav, které získáme po pěti hodech mincí, a jedná se o dobře vyváženou minci. Pak jsme spočítali pravděpodobnosti, které má tato náhodná proměnná u jednotlivých hodnot. Vypíšu je zde. Pravděpodobnost, že budu mít přesně jednu hlavu nebo nula hlav--začněme zde. Pravděpodobnost, že máme nul hlav je stejná jako pravděpodobnost, že padne pět orlů--to je 1 z 32. Pravděpodobnost, že bude 1 hlava je 5 z 32. Pravděpodobnost, že budou 2 hlavy--pravděpodobnost, že náhodná veličina bude mít hodnotu 2 bude co? Myslím, že vyšlo 10/32. Ano, bylo to 10/32 nebo 5/16. 10/32 se rovná 5/16. Pravděpodobnost, že budou tři hlavy, to bylo stejné, tj. 10/32, což se rovná 5/16. A to dává smysl, protože pravděpodobnost 3 hlav je stejná jako 2 orlů. Pravděpodobnost, že padnou 2 orli je stejná jako pravděpodobnost, že padnou 2 hlavy. A pak pravděpodobnost, že padnou 4 hlavy se rovná 5/32, což také dává smysl, neboť pravděpodobnost, že padnou 4 hlavy je stejná jako pravděpodobnost, že padne 1 orel. A 1 orel má stejnou pravděpodobnost jako 1 hlava. Jde o stejná čísla. A nakonec, pravděpodobnost, že padne 5 hlav je stejná jako žádný orel, tj. 1/32. Pravděpodobnost, že nepadnou žádní orli je stejná jako pravděpodobnost, že nepadnou žádné hlavy. Nakreslíme to. Nakreslíme rozdělení pravděpodobnosti. Toto je osa x. Je to příliš slabé. Udělám to v jiné barvě. Teď nakreslím osu y. Tak. Jaké jsou různé hodnoty, které nabývá náhodná proměnná? Jedná se o diskrétní hodnoty. Jsou to konečná čísla, která může náhodná proměnná nabýt. Jaká byla funkce definující náhodnou proměnnou? Tato náhodná proměnná, počet hlav po pěti hodech. Nemůže zde být nekončený počet různých hodnot. Hodnoty mohou být od 0 do 5. A musí se jednat o celá čísla. Důležité je, že existuje končený počet hodnot, které tato proměnná může nabývat. Proto se jedná o diskrétní rozdělení pravděpodobnosti. Takže, pravděpodobnost--nakreslím 0, 1, 2, 3, 4 a 5. To jsou hodnoty náhodné proměnné X. Toto je počet hlav v pěti hodech. Nejdřív nakreslím horní hodnoty. Horní hodnoty jsou zde. 10/32. To je pravděpodobnost 2 nebo 3, které jsou identické. Nakreslím sloupcový graf. 2 a 3; zde je 10/32. Nakreslím je nejvyšší, protože mají nejvyšší hodnoty. 2 a 3 jsou oba 10/32. Nakreslím to trochu jinak. Takže se budou dotýkat. Řekněme, že 2 je zde a pak nakreslím 3. A 3 je také zde. Tak. Jaká je pravděpodobnost, že dostanu 1? To bylo 5/32, takže 1/2 z nich. Tyto dva sloupce by měly mít stejnou výšku. 5/32. Takto. Což je stejné jako při 4 hlavách. Tak. Řekněme, že 4 je zde. Pravděpodobnost, že bude 0 nebo 5 je stejná. Takže 1. To bude 1/5 z této výšky. Takže to bude vypadat asi takto. Řekněme, že tento poslední sloupec je pro 5. Snad nejtěžší je to nakreslit. Bude to vypadat asi takto. Toto je pro 5 a toto pro 4. A toto zde je 10/32 nebo 5/16. Toto je 5/32. A zde je 1/32. Nakreslil jsem rozdělení binomické pravděpodobnosti. Je to zvláštní případ rozdělení binomické pravděpodobnosti. Budeme-li se blížit nekonečným hodnotám, pak získáme spojité rozdělení a přiblížíme se ke slavnému tvaru zvonu. Pak to začne vypadat jako zvon. Nebo takto. Možná to udělám v Excelu. Označíme to jako počet hlav v pěti hodech. Kdybych to udělal jako počet hlav v pěti milionech hodů. Pak by tyto sloupce byly velmi blízko sebe a začaly by se blížit k této křivce, ve tvaru zvonu. Toto je důležité rozdělení. Popisuje totiž velký díl náhodných procesů. Jedná se o důležitou statistiku, protože ve statistice obvykle není znám mechanismus, který vytváří výsledky. A tudíž se předpokládá, že se jedná o náhodnou veličinu. Pokud sečteme několik náhodných událostí. Získáme náhodné události podobné sčítání počtu hlav. A tam lze předpokládat, v diskrétním případě, binomické rozdělení. V několika dalších videích ukáži spojitá rozdělení, která představují normální rozdělení. Je důležité si uvědomit, že někdy lidé předpokládají určitě věci, které však mají negativní dopady zejména ve finanční oblasti. Předpokládají, že některé procesy mají binomické nebo normální rozdělení, přestože je ve skutečnosti nemají. Pokud předpokládáme binomické rozdělení tohoto způsobu, pak pravděpodobnosti na obou koncích budou opravdu malé. Ale pokud je rozdělení spíš takového tvaru? Budeme se tomu víc věnovat. Nebudeme postupovat příliš rychle. Obecně se dá říct, že je důležité pochopit předpoklady tvrzení, že se jedná o normální rozdělení. A my předpokládáme, že se jedná o binomické rozdělení. Uvidíme v budoucnu, proč je to důležité. Nyní se podíváme, co jsme již probrali. Proč se to nazývá binomické rozdělení? Když hodíme 5 mincemi, nebo 5 krát jednou mincí, pokaždé vyberu náhodné postavení hlav a orlů. Měl bych tomu říkat: v každé kombinaci hlav a orlů. Toto je jeden případ: pět hodů. Každý má přesně pravděpodobnost 1 z 32. Je 32 způsobů, jak zkombinovat hlavy a orly. Každá z nich má pravděpodobnost 1 z 32. V předchozím videu jsme zjistili pravděpodobnost přesně dvou hlav. V kolika případech je možné mít tuto kombinaci. Kolik permutací mají 2 hlavy? Spočítali jsme je a zjistili, že 10 z nich má 2 hlavy a proto byla pravděpodobnost 10 z 32. A na to jsme přišli pro případ 2 hlav. 1 z 5 hodů by mohl být první hlava a pak 1 ze 4 hodů by mohl být druhá hlava. Nezáleží nám na pořadí, nezáleží, jestli hod 1 byl první hlava a hod 2 byl druhá hlava, nebo obráceně. Takže jsme dělili 2, a to bylo identické jako faktoriál 5. Označím to barvou. Tato část je stejná jako faktoriál 5 nad faktoriálem 3. A pak, toto je stejné jako faktoriál 2, protože faktoriál 2 je 2 krát 1. Takže to lze napsat takto. Pravděpodobnost, že x se rovná n-- a toto je x, které jsem již definoval jako náhodnou proměnnou, a počet hlav, který získám při 5 hodech mincí--se rovná faktoriál 5 děleno faktoriál n. V tomto případě to bylo 2. 2 bylo n. Pravděpodobnost, že získám přesně 2 hlavy je krát 5 mínus faktoriál 2. Podívejte se na to prosím ještě jednou, protože je to klíčové. Pochopit intuitivně, o co zde jde. Doporučuji, abyste se podívali na videa, o pravděpodobnosti, týkající se binomických koeficientů a také o házení mincí a z něho odvozených problémů pravděpodobnosti. Tam se tomu věnuji do většího detailu. Pokud jste ta videa již viděli, nebo máte s touto oblastí zkušenost, poznáte, že se jedná o binomický koeficient. Ještě existuje video, které se nazývá binomické, protože tyto koeficienty se objeví, když násobíte binomické veličiny. Binomické veličiny jsou případy, ve kterých sčítáme x plus y a pak je násobíme, abychom získali různé mocniny. Jejich koeficienty pak--jsou prostě stejné. Na to jsem připravil celé video. A proto to funguje. A proto jim říkáme binomické koeficienty. A proto tomu říkáme binomické rozdělení. Také to můžeme napsat jako 5 nad n. A to proto, že jsme měli 5 hodů, ze kterých jsme vybírali 2 hodů, které byly hlavy. V tomto případě jsme měli pět hodů a vybírali jsme n hodů, které byly hlavy. To ukazuje kolik rozdílných permutací vyhovuje naší podmínce Jaká je pravděpodobnost každého z těchto případů? Je to krát 1 z 32. Proto se to nazývá binomické rozdělení. Každá hodnota pravděpodobnosti každé hodnoty náhodné proměnné se dá spočítat pomocí binomických koeficientů. Zase budeme končit. Uděláme ještě několik příkladů, protože musíme nejdříve pochopit binomické rozdělení. Pak se posuneme k normálnímu rozdělení. Na shledanou.
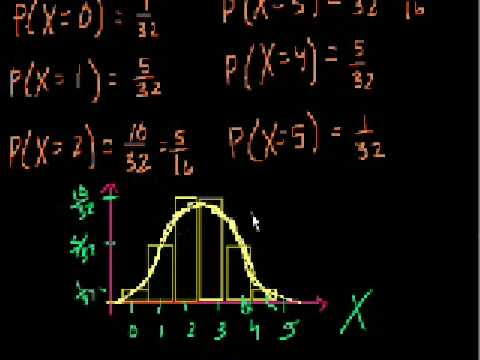
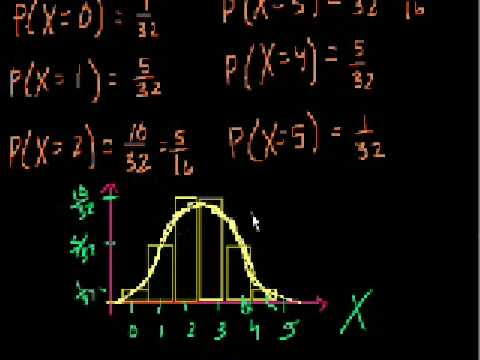
0:00
11:05